
【题目】如图,在平面直角坐标系中,△AOC的顶点坐标分别为A(2,2)、O(0,0)、C(![]() ,0),以原点O为位似中心.
,0),以原点O为位似中心.
(1)在第一象限内,相似比为![]() ,将△AOC缩小,不用画图,请直接写出缩小后的△A1OC1的两个顶点坐标:A1 ,C1 ;
,将△AOC缩小,不用画图,请直接写出缩小后的△A1OC1的两个顶点坐标:A1 ,C1 ;
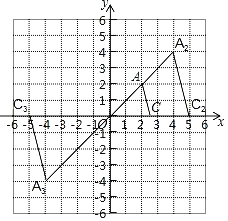
(2)相似比为2,将△AOC放大在第一象限画出放大后的△A2OC2,直接写出两个顶点的坐标:A2 ,C2 ;在第三象限画出放大后的△A3OC3,直接写出两个顶点的坐标:A3 ,C3 ;
(3)相似比为k,将△AOC放大,若△AOC边上有任意一点P的坐标为(x,y),则放大后的图形上,点P的对应点Q的坐标为 .(用含k、x和y的式子表示).
(建议:先用铅笔画图,确定无误后用黑色水性笔画在答题卡上)
【答案】(1)A1(1,1),C1(![]() ,0);(2)(4,4),(5,0),(﹣4,﹣4),(﹣5,0);(3)(kx,ky)或(﹣kx,﹣ky).
,0);(2)(4,4),(5,0),(﹣4,﹣4),(﹣5,0);(3)(kx,ky)或(﹣kx,﹣ky).
【解析】
(1)直接利用位似图形的性质进而得出对应点坐标;
(2)直接利用位似图形的性质进而得出对应点坐标;
(3)直接利用位似图形的性质进而得出对应点坐标.
解:(1)A1(1,1),C1(![]() ,0);
,0);
故答案为:(1,1),(![]() ,0);
,0);
(2)如图所示:A2(4,4),C2(5,0);A3(﹣4,﹣4),C3(﹣5,0);
故答案为:(4,4),(5,0),(﹣4,﹣4),(﹣5,0);
(3)相似比为k,将△AOC放大,若△AOC边上有任意一点P的坐标为(x,y),
则放大后的图形上,点P的对应点Q的坐标为:(kx,ky)或(﹣kx,﹣ky).
故答案为:(kx,ky)或(﹣kx,﹣ky).


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】重庆市旅游文化商店自制了一款文化衫,每件成本价为20元,每天销售150件:
(1)若要每天的利润不低于2250元,则销售单价至少为多少元?
(2)为了回馈广大游客,同时也为了提高这种文化衫的认知度,商店决定在“五一”节当天开展促销活动,若销售单价在(1)中的最低销售价的基础上再降低![]() m%,则日销售量可以在150件基础上增加
m%,则日销售量可以在150件基础上增加![]() m件,结果当天的销售额达到5670元;要使销售量尽可能大,求出m的值.
m件,结果当天的销售额达到5670元;要使销售量尽可能大,求出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 是等边三角形,D 为 CB 延长线上一点,E 为 BC 延长线上点.
(1)当 BD、BC 和 CE 满足什么条件时,△ADB∽△EAC?
(2)当△ADB∽△EAC 时,求∠DAE 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:将函数C的图象绕点P(0,n)旋转180°,得到新的函数C1的图象,我们称函数C1是函数C关于点P的相关函数.
例如:当n=1时,函数![]() 关于点P(0,1)的相关函数为
关于点P(0,1)的相关函数为![]() .
.
(1)当n=0时,
①二次函数y=x2关于点P的相关函数为 ;
②点A(2,3)在二次函数y=ax2﹣2ax+a(a≠0)关于点P的相关函数的图象上,求a的值;
(2)函数![]() 关于点P的相关函数是
关于点P的相关函数是![]() ,则n= ;
,则n= ;
(3)当![]() n﹣1≤x≤
n﹣1≤x≤![]() n+3时,函数
n+3时,函数![]() 的相关函数的最小值为7,求n的值.
的相关函数的最小值为7,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习完北师大教材九年级上册第四章第6节“利用相似三角形测高”后,数学兴趣小组的3名同学利用课余时间想要测量学校里两棵树的高度.在同一时刻的阳光下,他们合作完成了以下工作:
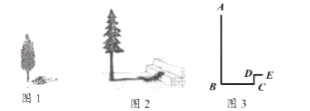
①测得一根长为l米的竹竿的影长为0.8米,甲树的影长为4.08米(如图l).
②测量的乙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上(如图2),测得落在地面上的影长为4.4米,一级台阶高为0.3米,落在第一级台阶的影子长为0.2米.
(1)在横线上直接填写甲树的高度为_____________米.
(2)图3为图2的示意图,请利用图3求出乙树的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
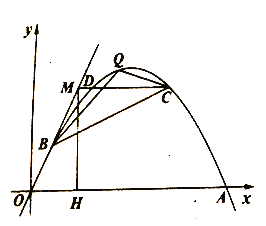
【题目】如图在平面直角坐标系![]() 中,二次函数
中,二次函数![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上点,点
是抛物线上点,点![]() 为射线
为射线![]() 上点(不含
上点(不含![]() 两点),且
两点),且![]() 轴于点
轴于点![]() .
.
(1)求直线![]() 及抛物线解析式;
及抛物线解析式;
(2)如图,过点![]() 作
作![]() 轴,且与抛物线交于
轴,且与抛物线交于![]() 两点(
两点(![]() 位于
位于![]() 左边),若
左边),若![]() ,点
,点![]() 为直线
为直线![]() 上方的抛物线上点,求
上方的抛物线上点,求![]() 面积的最大值,并求出此时点
面积的最大值,并求出此时点![]() 的坐标;
的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
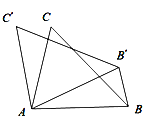
【题目】如图,在△ABC中,∠BAC=75°,以点A为旋转中心,将△ABC绕点A逆时针旋转,得△AB'C',连接BB',若BB'∥AC',则∠BAC′ 的度数是______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com