
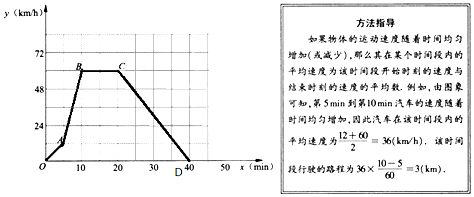
分析 (1)观察图象可知,第10min到20min之间的速度最高;
(2)设y=kx+b(k≠0),利用待定系数法求一次函数解析式解答,再把x=30代入函数关系式进行计算即可得解;
(3)用各时间段的平均速度乘以时间,求出行驶的总路程,再乘以每千米消耗的油量即可.
解答 解:(1)由图可知,第10min到20min之间的速度最高,为60km/h.
故答案为60;
(2)当20≤x≤40时,设y=kx+b(k≠0),
∵函数图象经过点(20,60),(40,0),
∴$\left\{\begin{array}{l}{20k+b=60}\\{40k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-3}\\{b=120}\end{array}\right.$,
所以,y与x的关系式为y=-3x+120,
当x=30时,y=30km/h;
(3)行驶的总路程
=$\frac{1}{2}$×(12+0)×$\frac{5}{60}$+$\frac{1}{2}$×(12+60)×$\frac{10-5}{60}$+60×$\frac{20-10}{60}$+$\frac{1}{2}$×(60+0)×$\frac{40-20}{60}$
=0.5+3+10+10
=23.5km,
∵汽车每行驶100km耗油10L,
∴小丽驾车从甲地到乙地共耗油:23.5×$\frac{10}{100}$=2.35升.
点评 本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,路程=速度×时间,从图形中准确获取信息是解题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:解答题
 如图,有一个边长为4cm的正方形和一个长为8cm、宽为4cm的长方形拼接成一个大长方形,现制作一个与大长方形面积相等的正方形,则这个大正方形的边长是多少?(结果保留小数点后两位)
如图,有一个边长为4cm的正方形和一个长为8cm、宽为4cm的长方形拼接成一个大长方形,现制作一个与大长方形面积相等的正方形,则这个大正方形的边长是多少?(结果保留小数点后两位)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
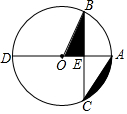 如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )
如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )| A. | $\frac{8}{9}π-\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{8}{9}π-\frac{{4\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{3}}}{18}π-\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{16}{9}π-\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com