
 如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,分析 (1)先证明四边形AEBD是平行四边形,再由矩形的性质得出DA=DB,即可证出四边形AEBD是菱形;
(2)连接DE,交AB于F,由菱形的性质得出AB与DE互相垂直平分,求出EF、AF,得出点E的坐标;设经过点E的反比例函数解析式为:y=$\frac{k}{x}$,把点E坐标代入求出k的值即可.
解答 (1)证明:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形,
∵四边形OABC是矩形,
∴DA=$\frac{1}{2}$AC,DB=$\frac{1}{2}$OB,AC=OB,
∴DA=DB,
∴四边形AEBD是菱形;
(2)解:连接DE,交AB于F,如图所示: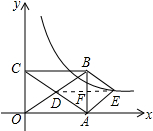 ∵四边形AEBD是菱形,
∵四边形AEBD是菱形,
∴AB与DE互相垂直平分,
∵OA=3,OC=2,
∴EF=DF=$\frac{1}{2}$OA=$\frac{3}{2}$,AF=$\frac{1}{2}$AB=1,3+$\frac{3}{2}$=$\frac{9}{2}$,
∴点E坐标为:($\frac{9}{2}$,1),
设经过点E的反比例函数解析式为:y=$\frac{k}{x}$,
把点E($\frac{9}{2}$,1)代入得:k=$\frac{9}{2}$,
∴经过点E的反比例函数解析式为:y=$\frac{9}{2x}$.
点评 本题是反比例函数综合题目,考查了平行四边形的判定、菱形的判定、矩形的性质、坐标与图形特征以及反比例函数解析式的求法;本题综合性强,有一定难度,特别是(2)中,需要作辅助线求出点E的坐标才能得出结果.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 1:2 | B. | 2:1 | C. | 1:4 | D. | 4:1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
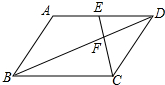 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )| A. | 3:2 | B. | 3:1 | C. | 1:1 | D. | 1:2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com