
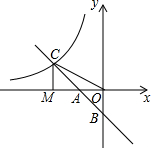
 如图,在直角坐标系中,直线y1=-x-l与坐标轴交于A,B两点,与双曲线y2=$\frac{k}{x}$交于点C,连结OC,过点C作CM⊥x轴,垂足为点M,且OA=AM.则下列结论正确的个数是( )
如图,在直角坐标系中,直线y1=-x-l与坐标轴交于A,B两点,与双曲线y2=$\frac{k}{x}$交于点C,连结OC,过点C作CM⊥x轴,垂足为点M,且OA=AM.则下列结论正确的个数是( ) | A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由直线可求得A点坐标,结合条件可求得M点、C点坐标,从而可求得k的值,利用反比例函数k的几何意义可判断①;利用函数的增减性可判断②,利用方程、函数和函数图象的交点的个数之间的关系可判断③;结合图象可判断④.
解答 解:
在y1=-x-l中,令y1=0可得x=-1,
∴A点坐标为(-1,0),
∵OA=AM,
∴OM=2,
∴M点坐标为(-2,0),
∵CM⊥x轴,且C点在双曲线上,
∴C点坐标为(-2,$\frac{k}{-2}$),
又点C在直线上,
∴$\frac{k}{-2}$=2-1,解得k=-2,
∴反比例函数解析式为y2=-$\frac{2}{x}$,
∴S△COM=$\frac{1}{2}$|k|=1,
故①正确;
在y1=-x-l中,-1<0,在y2=-$\frac{2}{x}$中,-2<0,
∴y1隨x的增大而减小,y2随x的增大而増大;
故②正确;
由两函数图象交于点C,且C点横坐标为-2,
∴方程-x-1=$\frac{k}{x}$有一个解为x=-2,
故③正确;
结合两函数图象可知,
当-2<x<0时,直线在双曲线的下方,
∴yl<y2,
故④正确;
综上可知正确的有四个,
故选D.
点评 本题主要考查函数图象的交点问题,掌握函数图象的交点坐标即对应两解析式构成的方程组的解是解题的关键.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 抽取的乒乓球数n | 50 | 100 | 200 | 500 | 1000 | 1500 | 2000 |
| 优等品的频数m | 48 | 95 | 188 | 471 | 946 | 1426 | 1898 |
| 优等品的频率$\frac{m}{n}$ | 0.960 | 0.950 | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
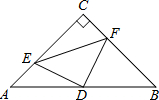 如图,△ABC是等腰三角形,∠C=90°,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:
如图,△ABC是等腰三角形,∠C=90°,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
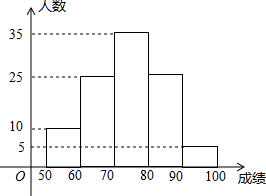 某校八年级同学进行物理知识竞赛,从中随机抽取100人的成绩进行整理,每个小组的分组标准是:50≤x<60,60≤x<70…,画出频数分布直方图如下:
某校八年级同学进行物理知识竞赛,从中随机抽取100人的成绩进行整理,每个小组的分组标准是:50≤x<60,60≤x<70…,画出频数分布直方图如下:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,直线EF绕对角线AC的中点O旋转,分别交BC、AD于E、F两点,连接AE、CF.
如图,在平行四边形ABCD中,直线EF绕对角线AC的中点O旋转,分别交BC、AD于E、F两点,连接AE、CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 2n枚 | B. | (n2+1)枚 | C. | (n2-n)枚 | D. | (n2+n)枚 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com