
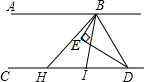
 如图,已知,BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.
如图,已知,BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.分析 (1)根据角平分线的定义可得∠ABD=2∠EBD,∠BDC=2∠BDE,然后求出∠ABD+∠BDC=180°,再根据同旁内角互补,两直线平行证明;
(2)根据角平分线的定义可得∠ABD=2∠EBD,∠HBD=2∠IBD,然后分点H在点D的左边和右边两种情况,表示出∠ABH和∠EBI,从而得解.
解答 (1)证明:∵BE平分∠ABD,DE平分∠BDC,
∴∠ABD=2∠EBD,∠BDC=2∠BDE,
∵∠EBD+∠EDB=90°,
∴∠ABD+∠BDC=2×90°=180°,
∴AB∥CD;
(2)解:∵BE平分∠ABD,
∴∠ABD=2∠EBD,
∵BI平分∠HBD,
∴∠HBD=2∠IBD,
如图1,点H在点D的左边时,∠ABH=∠ABD-∠HBD,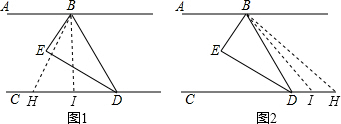
∠EBI=∠EBD-∠IBD,
∴∠ABH=2∠EBI,
∵AB∥CD,
∴∠BHD=∠ABH,
∴∠BHD=2∠EBI,
∴∠EBI=$\frac{1}{2}$∠BHD=28°,
如图2,点H在点D的右边时,∠ABH=∠ABD+∠HBD,
∠EBI=∠EBD+∠IBD,
∴∠ABH=2∠EBI,
∵AB∥CD,
∴∠BHD=180°-∠ABH,
∴∠BHD=180°-2∠EBI,
∴∠EBI=$\frac{1}{2}$(180°-∠BHD)=62°,
综上所述,∠EBI=28°或∠EBI=62°.
点评 本题考查了平行线的性质,角平分线的定义,熟记性质是解题的关键,难点在于(2)分情况讨论并理清图中各角度之间的关系.


科目:初中数学 来源: 题型:填空题
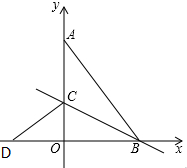 如图,在平面直角坐标系中,点A(0,8),B(6,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点D处,折痕所在的直线交y轴正半轴于点C,则直线DC的解析式为y=$\frac{3}{4}$x+3.
如图,在平面直角坐标系中,点A(0,8),B(6,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点D处,折痕所在的直线交y轴正半轴于点C,则直线DC的解析式为y=$\frac{3}{4}$x+3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次课堂调研数学试卷(解析版) 题型:解答题
已知:如图①、②,解答下面各题:

(1)图①中,∠AOB=55°,点P在∠AOB内部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,求∠EPF的度数。
(2)图②中,点P在∠AOB外部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,那么∠P与∠O有什么关系?为什么?
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?
(4)如果一个角的两边分别平行于另一个角的两边,则这两个角是什么关系?(请画图说明结果,不需要过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com