
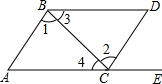
 如图,点E在AC的延长线上,对于下列给出的四个条件:
如图,点E在AC的延长线上,对于下列给出的四个条件: 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
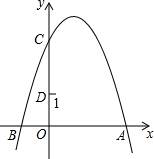 如图,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,则点P的坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).
如图,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,则点P的坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
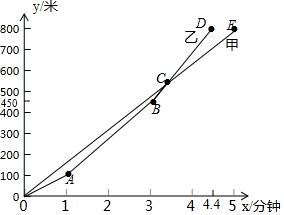 百舸竞渡,激情飞扬.为纪念爱国诗人屈原,某市举行龙舟赛.甲、乙两支龙舟队在比赛时,路程y(米)与时间x(分钟)之间的函数图象如图所示,根据图象回答下列问题:
百舸竞渡,激情飞扬.为纪念爱国诗人屈原,某市举行龙舟赛.甲、乙两支龙舟队在比赛时,路程y(米)与时间x(分钟)之间的函数图象如图所示,根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
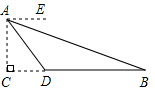 为了测量校园池塘B,D两地之间的距离,从距离地面高度为20米的教学楼A处测得点B的俯角∠EAB=15°,点D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求池塘B,D两地之间的距离(结果保留整数米).(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
为了测量校园池塘B,D两地之间的距离,从距离地面高度为20米的教学楼A处测得点B的俯角∠EAB=15°,点D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求池塘B,D两地之间的距离(结果保留整数米).(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com