
【题目】已知,在平行四边形ABCD中,E为AD上一点,且AB=AE,连接BE交AC于点H,过点A作AF⊥BC于F,交BE于点G.
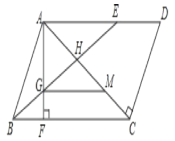
(1)若∠D=50°,求∠EBC的度数;
(2)若AC⊥CD,过点G作GM∥BC交AC于点M,求证:AH=MC.
【答案】(1)∠EBC=25°;(2)见解析;
【解析】
(1)根据等边对等角以及平行线的性质,即可得到∠1=∠2=![]() ∠ABC,再根据平行四边形ABCD中,∠D=50°=∠ABC,可得出∠EBC的度数;
∠ABC,再根据平行四边形ABCD中,∠D=50°=∠ABC,可得出∠EBC的度数;
(2)过M作MN⊥BC于N,过G作GP⊥AB于P,则∠CNM=∠APG=90°,先根据AAS判定△BPG≌△BFG,得到PG=GF,根据矩形GFNM中GF=MN,即可得出PG=NM,进而判定△PAG≌△NCM(AAS),可得AG=CM,再根据等角对等边得到AH=AG,即可得到结论.
(1)∵AB=AE,
∴∠1=∠3,
∵AE∥BC,
∴∠2=∠3,
∴∠1=∠2=![]() ∠ABC,
∠ABC,
又∵平行四边形ABCD中,∠D=50°,
∴∠ABC=50°,
∴∠EBC=25°;
(2)证明:如图,过M作MN⊥BC于N,过G作GP⊥AB于P,则∠CNM=∠APG=90°,
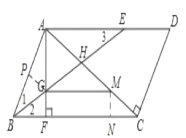
由(1)可得,∠1=∠2,
∵AF⊥BC,
∴∠BPG=∠BFG=90°,
在△BPG和△BFG中,
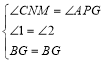 ,
,
∴△BPG≌△BFG(AAS),
∴PG=GF,
又∵矩形GFNM中,GF=MN,
∴PG=NM,
∵AC⊥CD,CD∥AB,
∴∠BAC=90°=∠AFB,
即∠PAG+∠ABF=∠NCM+∠ABC=90°,
∴∠PAG=∠NCM,
在△PAG和△NCM中,
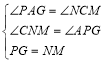 ,
,
∴△PAG≌△NCM(AAS),
∴AG=CM,
∵∠1=∠2,∠BAH=∠BFG,
∴∠AHG=∠FGB=∠AGH,
∴AG=AH,
∴AH=MC.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
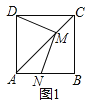
【题目】如图1,点M放在正方形ABCD的对角线AC(不与点A重合)上滑动,连结DM,做MN⊥DM,交直线AB于N.
(1)求证:DM=MN;
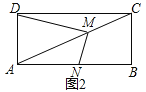
(2)若将(1)中的正方形变为矩形,其余条件不变如图,且DC=2AD,求MD:MN的值;
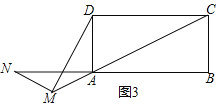
(3)在(2)中,若CD=nAD,当M滑动到CA的延长线上时(如图3),请你直接写出MD:MN的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
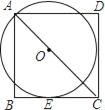
【题目】如图,O为正方形ABCD对角线上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E.
(1)求证:CD是⊙O的切线;
(2)若正方形ABCD的边长为10,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知圆锥底面半径r=10cm,母线长为40cm.

(1)求它的侧面展开图的圆心角和表面积.
(2)若一只甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是多少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
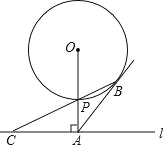
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知M=3a2-2ab+b2 , N=2a2+ab-3b2
(1)化简2M-3N;
(2)若2(7a-1)2+3|b+1|=0,求2M-3N的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图A1、A2、A3....在直线y=x上,点C1、C2、C3....在直线y=2x上,以它们为顶点依次构造第一个正方形A1C1A2B1,第二个正方形A2C2A3B2...,若A1的横坐标是1,则B3的坐标是__________,第n个正方形的面积是__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com