
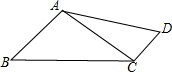
 四边形ABCD中,∠B=∠D,∠BAC=120°,∠BCD=150°,若AC=5$\sqrt{3}$,AD=11,则BC的长为7$\sqrt{3}$.
四边形ABCD中,∠B=∠D,∠BAC=120°,∠BCD=150°,若AC=5$\sqrt{3}$,AD=11,则BC的长为7$\sqrt{3}$. 分析 延长BA,过点C作CE⊥BA与点E,延长DC,过点A做AF⊥DC与点F,在Rt△AEC中可得到$\frac{AC}{BC}$=$\frac{sin∠B}{sin∠BAC}$;在Rt△ACF中可得到$\frac{AC}{AD}$=$\frac{sin∠D}{sin∠ACD}$,再由∠ACD=∠BCD-∠ACB,结合已知角的度数,即可用∠D将∠ACD表示出来,在$\frac{AC}{AD}$=$\frac{sin∠D}{sin∠ACD}$中结合sin2∠D+cos2∠D=1,即可求出sin∠D=$\frac{5\sqrt{3}}{14}$=sin∠B,将其代入$\frac{AC}{BC}$=$\frac{sin∠B}{sin∠BAC}$中即可求出线段BC的长.
解答 解:延长BA,过点C作CE⊥BA与点E,延长DC,过点A做AF⊥DC与点F,如图所示.
∵在Rt△AEC中,CE=AC•sin∠CAE=AC•sin∠BAC,CE=BC•sin∠B,
∴$\frac{AC}{BC}$=$\frac{sin∠B}{sin∠BAC}$.
∵在Rt△ACF中,AF=AC•sin∠ACF=AC•sin∠ACD,AF=AD•sin∠D,
∴$\frac{AC}{AD}$=$\frac{sin∠D}{sin∠ACD}$.
在△ABC中,∠ACB=180°-∠B-∠BAC,
∵∠BAC=120°,
∴∠ACB=60°-∠B.
∵∠BCD=150°,∠B=∠D,
∴∠ACD=∠BCD-∠ACB=150°-(60°-∠B)=90°+∠B=90°+∠D.
∴$\frac{AC}{AD}$=$\frac{sin∠D}{sin∠ACD}$=$\frac{sin∠D}{sin(90°+∠D)}$=$\frac{sin∠D}{cos∠D}$,
∵AC=5$\sqrt{3}$,AD=11,
∴sin∠D=$\frac{5\sqrt{3}}{11}$cos∠D,
又∵sin2∠D+cos2∠D=1,
∴sin∠D=$\frac{5\sqrt{3}}{14}$=sin∠B.
又∵$\frac{AC}{BC}$=$\frac{sin∠B}{sin∠BAC}$,且∠BAC=120°,AC=5$\sqrt{3}$,
∴BC=$\frac{AC•sin∠BAC}{sin∠B}$=$\frac{5\sqrt{3}×\frac{\sqrt{3}}{2}}{\frac{5\sqrt{3}}{14}}$=7$\sqrt{3}$.
故答案为:7$\sqrt{3}$.
点评 本题考查了解直角三角形,解题的关键是:借助直角三角形这个工具得出$\frac{AC}{BC}$=$\frac{sin∠B}{sin∠BAC}$以及$\frac{AC}{AD}$=$\frac{sin∠D}{sin∠ACD}$.


科目:初中数学 来源: 题型:填空题
 如图,一只蜘蛛在一个正方形框架(每个方格都是正方向)的A处,一只苍蝇在这个正方形框架的B处,这只蜘蛛要袭击这只苍蝇(它必须沿正方形框架线路爬行).那么它袭击苍蝇的最佳路线有6条.
如图,一只蜘蛛在一个正方形框架(每个方格都是正方向)的A处,一只苍蝇在这个正方形框架的B处,这只蜘蛛要袭击这只苍蝇(它必须沿正方形框架线路爬行).那么它袭击苍蝇的最佳路线有6条.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在小岛上有一观察站A,据测,灯塔B在观察站A北偏西48°的方向,灯塔C在B正东方向,且相距10海里,灯塔C与观察站A相距15海里,请你测算灯塔C处在观察站A的什么方向.(精确到0.1°)
如图,在小岛上有一观察站A,据测,灯塔B在观察站A北偏西48°的方向,灯塔C在B正东方向,且相距10海里,灯塔C与观察站A相距15海里,请你测算灯塔C处在观察站A的什么方向.(精确到0.1°)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,直线AB:y=-x+b交y轴于点A(0,4),交x轴于点B.
如图,平面直角坐标系中,直线AB:y=-x+b交y轴于点A(0,4),交x轴于点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com