
【题目】如图,有一个形如六边形的点阵,它的中心是一个点,算做第一层,第二层每边两个点,第三层每边三个点,以此类推.

(1)填写下表
层数 | 1 | 2 | 3 | 4 | 5 |
该层对应的点数 | 1 | 6 | 12 |
(2)写出第n层对应的点数(n≥2);
(3)如果某层一共有72个点,请你求出对应的层数.
【答案】(1)18,24;(2) 6(n-1)(n≥2);见解析.(3)13.
【解析】(1)观察图形中点的排列规律得到第一层对应的点数为1,第二层对应的点数为6×2-6=6,第三层对应的点数为6×3-6=12,则第四层对应的点数为6×4-6=18,第五层对应的点数为6×5-6=24;
(2)第n层对应的点数为6(n-1)(n≥2);
(3)利用(2)的结论得到6(n-1)=72,然后解方程即可.
(1)第一层对应的点数为1,第二层对应的点数为6×2-6=6,第三层对应的点数为6×3-6=12,
则第四层对应的点数为6×4-6=18,第五层对应的点数为6×5-6=24;
故答案为18,24;
(2)第n层对应的点数为6(n-1)(n≥2);
(3)设72个点所对应的层数为n,
根据(2)的结论得6(n-1)=72,解得n=13,
即第13层对应的点数为72.


科目:初中数学 来源: 题型:
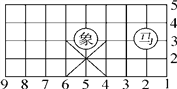
【题目】如图是中国象棋棋盘的一部分,棋盘中“马”所在的位置用(2,3)表示.
(1)图中“象”的位置可表示为____________;
(2)根据象棋的走子规则,“马”只能从“日”字的一角走到与它相对的另一角;“象”只能从“田”字的一角走到与它相对的另一角.请按此规则分别写出“马”和“象”下一步可以到达的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移 ![]() 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
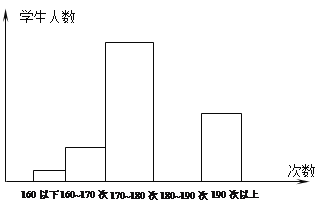
【题目】为了解中学生的体能情况,某校抽取了50名八年级学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频数分布直方图如下图所示已知图中从左到右前第一、第二、第三、第五小组的频率分别为0.04 , 0.12 ,0.4 ,O.28 ,根据已知条件解答下列问题:
(1)第四个小组的频率是多少? 你是怎样得到的?
(2)这五小组的频数各是多少?
(3)在这次跳绳中,跳绳次数的中位数落在第几小组内?
(4)将频数分布直方图补全,并分别写出各个小组的频数,并画出频数分布折线图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区调查社区居民双休日的学习状况,采取下列调查方式:①从一幢高层住宅楼中选取200名居民;②从不同住层楼中随机选取200名居民;③选取社区内的200名在校学生.

(1)上述调查方式最合理的是 (填序号);
(2)将最合理的调查方式得到的数据制成扇形统计图(如图①)和频数分布直方图(如图②).
①请补全直方图(直接画在图②中);
②在这次调查中,200名居民中,在家学习的有 人;
(3)请估计该社区2000名居民中双休日学习时间不少于![]() 的人数.
的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A,B,C,回答下列问题:
(1)若将点B向右移动6个单位后,三个点所表示的数中最小的数是多少?
(2)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(3)在点B左侧找一点E,使点E到点A的距离是到点B的距离的2倍,并写出点E表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老王的房子准备开始装修,请来师徒二人做泥水.已知师傅单独完成需10天,徒弟单独完成需15天。
(1)若两人先合作2天,剩下的由徒弟单独做,结果超出老王预期的工期3天完成,求老王预期的工期天数;
(2)若师傅的工价每天300元,徒弟的工价每天220元,老王房子的泥水工价预算不超过3180元,问师傅至少要做几天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入![]() 表是某周的生产情况
表是某周的生产情况![]() 超产为正、减产为负
超产为正、减产为负![]() :
:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
![]() 根据记录可知前三天共生产多少辆;
根据记录可知前三天共生产多少辆;
![]() 产量最多的一天比产量最少的一天多生产多少辆;
产量最多的一天比产量最少的一天多生产多少辆;
![]() 该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个正整数能表示为两个正整数的平方差,则称这个正整数为“智慧数”(如3=22-12,16=52-32,则3和16是智慧数).已知按从小到大的顺序构成如下数列:3,5,7,8,9,11,12,13,15,16,17,19,20,21,23,24,25,…则第2 013个“智慧数”是______.
【答案】2 687
【解析】解析:观察数的变化规律,可知全部“智慧数”从小到大可按每三个数分一组,从第2组开始每组的第一个数都是4的倍数,归纳可得,第n组的第一个数为4n(n≥2).因为2 013÷3=671,所以第2 013个“智慧数”是第671组中的第3个数,即为4×671+3=2 687.
点睛:找规律题需要记忆常见数列
1,2,3,4……n
1,3,5,7……2n-1
2,4,6,8……2n
2,4,8,16,32……![]()
1,4,9,16,25……![]()
2,6,12,20……n(n+1)
一般题目中的数列是利用常见数列变形而来,其中后一项比前一项多一个常数,是等差数列,列举找规律.后一项是前一项的固定倍数,则是等比数列,列举找规律.
【题型】填空题
【结束】
19
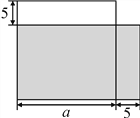
【题目】如图,郑某把一块边长为a m的正方形的土地租给李某种植,他对李某说:“我把你这块地的一边减少5 m,另一边增加5 m,继续租给你,你也没有吃亏,你看如何”.李某一听,觉得自己好像没有吃亏,就答应了.同学们,你们觉得李某有没有吃亏?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com