
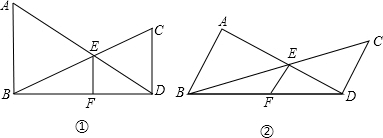
分析 (1)易证EF∥AB∥CD,则△ABD∽△EFD,根据相似三角形的对应边的比相等,即可证得$\frac{EF}{AB}$=$\frac{DF}{BD}$,同理$\frac{EF}{CD}$=$\frac{BF}{BD}$,两式相加即可得;
(2)由题意知,两直线平行是很关键的条件,要根据三角形平行线分线段成比例,找出关系,然后相加就得到结果;
(3)要用到第一问的结论,作出各个三角形的高,再把各面积用边表示出来,即可找到关系.
解答 解:
(1)$\frac{1}{AB}$+$\frac{1}{CD}$=$\frac{1}{EF}$,
证明如下:
∵AB⊥BD,EF⊥BD,
∴EF∥AB,
∴△ABD∽△EFD,
∴$\frac{EF}{AB}$=$\frac{DF}{BD}$,同理$\frac{EF}{CD}$=$\frac{BF}{BD}$,
∴$\frac{EF}{AB}$+$\frac{EF}{CD}$=$\frac{DF}{BD}$+$\frac{BF}{BD}$=$\frac{DF+BF}{BD}$=$\frac{BD}{BD}$=1,即($\frac{1}{AB}$+$\frac{1}{CD}$)•EF=1,
∴$\frac{1}{AB}$+$\frac{1}{CD}$=$\frac{1}{EF}$;
(2)成立.
理由如下:
∵AB∥EF,
∴$\frac{EF}{AB}$=$\frac{DF}{BD}$,
∵CD∥EF,
∴$\frac{EF}{CD}$=$\frac{BF}{BD}$,
∴$\frac{EF}{AB}$+$\frac{EF}{CD}$=$\frac{DF}{BD}$+$\frac{BF}{BD}$=$\frac{DF+BF}{BD}$=$\frac{BD}{BD}$=1,即($\frac{1}{AB}$+$\frac{1}{CD}$)•EF=1,
∴$\frac{1}{AB}$+$\frac{1}{CD}$=$\frac{1}{EF}$;
(3)关系式为:$\frac{1}{{S}_{△ABD}}$+$\frac{1}{{S}_{△BDC}}$=$\frac{1}{{S}_{△BED}}$.
证明如下:
如图,分别过A作AM⊥BD于M,过E作EN⊥BD于N,过C作CK⊥BD交BD的延长线于K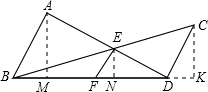
由(1)可得:$\frac{1}{AM}$+$\frac{1}{CK}$=$\frac{1}{EN}$,
∴$\frac{2}{BD•AM}$+$\frac{2}{BD•CK}$=$\frac{2}{BD•EN}$,即$\frac{1}{\frac{1}{2}BD•AM}$+$\frac{1}{\frac{1}{2}BD•CK}$=$\frac{1}{\frac{1}{2}BD•EN}$,
又∵$\frac{1}{2}$BD•AM=S△ABD,$\frac{1}{2}$BD•CK=S△BCD,$\frac{1}{2}$BD•EN=S△BED,
∴$\frac{1}{{S}_{△ABD}}$+$\frac{1}{{S}_{△BDC}}$=$\frac{1}{{S}_{△BED}}$.
点评 本题主要考查了相似三角形的判定与性质,正确通过相似三角形的性质把线段的比进行转化是关键.同时考查了平行线分线段成比例定理的运用.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:选择题
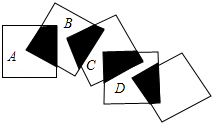 将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和是( )cm2.
将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和是( )cm2.| A. | 2cm2 | B. | 4cm2 | C. | 6cm2 | D. | 8cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
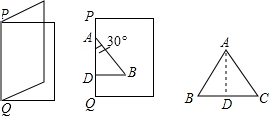 如图,欢欢将一张白纸对折,折痕为PQ.以PQ上的线段AD为一条直角边画出直角三角形ABD,使∠DAB=30°,沿折线DBA剪下三角形纸片,将其打开展平,得到△ABC.
如图,欢欢将一张白纸对折,折痕为PQ.以PQ上的线段AD为一条直角边画出直角三角形ABD,使∠DAB=30°,沿折线DBA剪下三角形纸片,将其打开展平,得到△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12 个 | B. | 15 个 | C. | 9 个 | D. | 10 个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
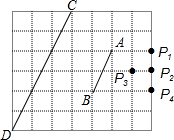 如图6×7的方格中,点A,B,C,D是格点,线段CD是由线段AB位似放大得到的,则它们的位似中心是( )
如图6×7的方格中,点A,B,C,D是格点,线段CD是由线段AB位似放大得到的,则它们的位似中心是( )| A. | P1 | B. | P2 | C. | P3 | D. | P4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com