
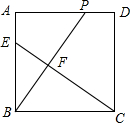
 如图所示,正方形ABCD中,AB=1,点E从点B出发到点A做匀速运动,点P从点D开始到点A做匀速运动,且BP⊥CE,垂足为点F,连接PE.
如图所示,正方形ABCD中,AB=1,点E从点B出发到点A做匀速运动,点P从点D开始到点A做匀速运动,且BP⊥CE,垂足为点F,连接PE.分析 (1)证明△BFC∽△PAB,根据相似三角形的性质得到比例式,计算即可;
(2)证明△BAP≌△CBE,根据全等三角形的性质得到CE=BP,根据题意列出方程,解方程即可;
(3)根据相似三角形的性质列出比例式,计算即可.
解答 解:(1)∵BP⊥CE,
∴∠FEB+∠FBE=90°,
∵∠ABC=90°,
∴∠FEB+∠BCE=90°,
∴∠BCE=∠FBE,又∠BFC=∠PAB=90°,
∴△BFC∽△PAB,
∴$\frac{CF}{AB}$=$\frac{BC}{BP}$,即$\frac{y}{1}$=$\frac{1}{x}$,
整理得,y=$\frac{1}{x}$,(1≤x≤$\sqrt{2}$);
(2)在△BAP和△CBE中,
$\left\{\begin{array}{l}{∠ABP=∠BCE}\\{AB=BC}\\{∠BAP=∠CBE}\end{array}\right.$,
∴△BAP≌△CBE,
∴CE=BP=x,
∵CF=2EF,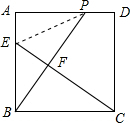
∴y=$\frac{2}{3}$x,又y=$\frac{1}{x}$,
解得,x=$\frac{\sqrt{6}}{2}$,
答:BP=$\frac{\sqrt{6}}{2}$;
(3)由(2)得,△BAP≌△CBE,
∴BE=AP,
设AP=x,则BE=x,AE=1-x,
当△AEP∽△BCE时,$\frac{AE}{BC}$=$\frac{AP}{BE}$,即$\frac{1-x}{1}$=1,
解得,x=0;
当△AEP∽△BEC时,$\frac{AP}{BC}$=$\frac{AE}{BE}$,即$\frac{x}{1}$=$\frac{1-x}{x}$,
解得,x=$\frac{\sqrt{5}-1}{2}$.
∴当AP=$\frac{\sqrt{5}-1}{2}$时,△AEP与△BEC相似.
点评 本题考查的是相似三角形的性质、掌握相似三角形的判定定理和性质定理是解题的关键,解答时,注意分情况讨论思想的灵活运用.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
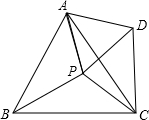 如图,P是等边三角形ABC内一点,∠APB、∠BPC、∠CPA的度数比为4:5:6,以AP为边作正△APD,连接DC,则△PDC的三个内角度数从小到大的比为3:5:9.
如图,P是等边三角形ABC内一点,∠APB、∠BPC、∠CPA的度数比为4:5:6,以AP为边作正△APD,连接DC,则△PDC的三个内角度数从小到大的比为3:5:9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
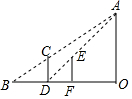 如图,墨墨和茗茗在晚上利用灯光下自己的影长来测量路灯AO的高度,当墨墨在点D处时.茗茗测得墨墨的身高CD与影子BD的长正好相等,接着墨墨沿BO方向走,走到点F处时,墨墨身高EF的影子恰好是线段DF.已知DF=1.2m,墨墨的身高为1.8m,则路灯AO的高度为( )
如图,墨墨和茗茗在晚上利用灯光下自己的影长来测量路灯AO的高度,当墨墨在点D处时.茗茗测得墨墨的身高CD与影子BD的长正好相等,接着墨墨沿BO方向走,走到点F处时,墨墨身高EF的影子恰好是线段DF.已知DF=1.2m,墨墨的身高为1.8m,则路灯AO的高度为( )| A. | 5m | B. | 5.4m | C. | 5.6m | D. | 5.8m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com