
分析 原式利用拆项法变形,计算即可得到结果.
解答 解:原式=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{4}$-$\frac{1}{6}$+$\frac{1}{5}$-$\frac{1}{7}$+$\frac{1}{6}$-$\frac{1}{8}$+$\frac{1}{7}$-$\frac{1}{9}$+$\frac{1}{8}$-$\frac{1}{10}$+$\frac{1}{9}$-$\frac{1}{11}$+$\frac{1}{10}$-$\frac{1}{12}$+$\frac{1}{11}$-$\frac{1}{13}$+$\frac{1}{12}$-$\frac{1}{14}$+$\frac{1}{13}$-$\frac{1}{15}$+$\frac{1}{14}$-$\frac{1}{16}$+$\frac{1}{15}$-$\frac{1}{17}$+$\frac{1}{16}$-$\frac{1}{18}$+$\frac{1}{17}$-$\frac{1}{19}$+$\frac{1}{18}$-$\frac{1}{20}$)
=$\frac{1}{2}$($\frac{3}{2}$-$\frac{1}{20}$)=$\frac{29}{40}$,
故答案为:$\frac{29}{40}$
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:选择题
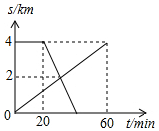 已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,芳芳到达A地时间为( )
已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,芳芳到达A地时间为( )| A. | 8:30 | B. | 8:35 | C. | 8:40 | D. | 8:45 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 8 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2cm,13cm,13cm | B. | 4cm,4cm,4cm | C. | 3cm,4cm,7cm | D. | 1cm,$\sqrt{2}$ cm,$\sqrt{3}$ cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+1)(x-1)=x2-1 | B. | x2-2x+1=x(x-2)+1 | C. | x2-4y2=(x-2y)2 | D. | 2x2+4x+2=2(x+1)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
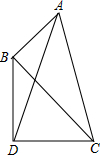 将一副三角板如图摆放在一起,连接AD,则∠ADB的正切值为( )
将一副三角板如图摆放在一起,连接AD,则∠ADB的正切值为( )| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$+1 | C. | $\frac{\sqrt{3}+1}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△ACD,点O、B对应点分别是C、D.
平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△ACD,点O、B对应点分别是C、D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com