
【题目】在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).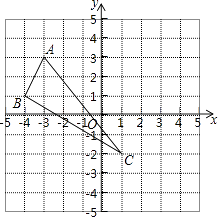
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法).
(2)直接写出A′、B′、C′三点的坐标:
A′( , ); B′( , );
C′( , ).
(3)求△ABC的面积.
 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如果a是b的近似值,那么我们把b叫做a的真值.若用四舍五入法得到的近似数是85,则下列各数不可能是其真值的是( )
A. 85.01 B. 84.51 C. 84.99 D. 84.49
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题不一定成立的是( )
A.斜边与一条直角边对应成比例的两个直角三角形相似;
B.两个等腰直角三角形相似;
C.两边对应成比例且有一个角相等的两个三角形相似;
D.各有一个角等于95°的两个等腰三角形相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,BC∥OA,∠B=∠A=100°,试回答下列问题:
(1)如图1所示,求证:OB∥AC; 
(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.试求∠EOC的度数; 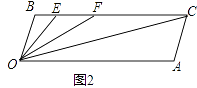
(3)在(2)的条件下,若平行移动AC,如图3,则∠OCB:∠OFB的值是 . 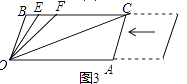
查看答案和解析>>
科目:初中数学 来源: 题型:
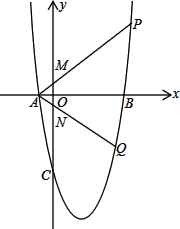
【题目】如图1,在平面直角坐标系中,抛物线y=x2-4x-5与x轴分别交于A、B(A在B的左边),与y轴交于点C,直线AP与y轴正半轴交于点M,交抛物线于点P,直线AQ与y轴负半轴交于点N,交抛物线于点Q,且OM=ON,过P、Q作直线l
(1) 探究与猜想:
① 取点M(0,1),直接写出直线l的解析式
取点M(0,2),直接写出直线l的解析式
② 猜想:
我们猜想直线l的解析式y=kx+b中,k总为定值,定值k为__________,请取M的纵坐标为n,验证你的猜想
(2) 如图2,连接BP、BQ.若△ABP的面积等于△ABQ的面积的3倍,试求出直线l的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数. 小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.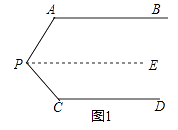
(1)按小明的思路,易求得∠APC的度数为度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由; 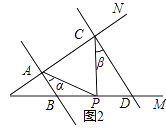
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com