
如图,在平面直角坐标系中,一次函数 (k≠0)的图象与反比例函数
(k≠0)的图象与反比例函数 (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且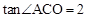 .
.
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)在x轴上求点E,使△ACE为直角三角形.(直接写出点E的坐标)
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:解答题
如图,已知矩形OABC中,OA=2,AB=4,双曲线 (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.
(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,请证明△EGD∽△DCF,并求出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,等腰梯形ABCD放置在平面直角坐标系中,已知A(-2,0)、B(6,0)、A(0,3),反比例函数的图象经过点C.
(1)求C点坐标和反比例函数的解析式;(6分)
(2)将等腰梯形ABCD向上平移 个单位后,使点B恰好落在双曲线上,求
个单位后,使点B恰好落在双曲线上,求 的值.(4分)
的值.(4分)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数 的图象经过点C,一次函数
的图象经过点C,一次函数 的图象经过点C,一次函数
的图象经过点C,一次函数 的图象经过点A,
的图象经过点A,
(1)求反比例函数与一次函数的解析式;
(2)求点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知反比例函数 (k为常数,k≠0)的图象经过点A(2,3).
(k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的解析式;
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,点A(1,a)在反比例函数 (x>0)的图象上,AB垂直于x轴,垂足为点B,将△ABO沿x轴向右平移2个单位长度,得到Rt△DEF,点D落在反比例函数
(x>0)的图象上,AB垂直于x轴,垂足为点B,将△ABO沿x轴向右平移2个单位长度,得到Rt△DEF,点D落在反比例函数 (x>0)的图象上.
(x>0)的图象上.
(1)求点A的坐标;
(2)求k值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数 的图象有一个交点A(m,2).
的图象有一个交点A(m,2).
(1)求m的值;
(2)求正比例函数y=kx的解析式;
(3)试判断点B(2,3)是否在正比例函数图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某公司从2009年开始投入技术改造资金,经技术改进后,其产品的生产成本不断降低,具体数据如表:
| 年度 | 2009 | 2010 | 2011 | 2012 |
| 投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(1)(4分)左下图是有几个大小完全一样的小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,请你画出该几何体的主视图和左视图.

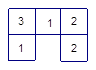
|
|
 的边OB上的一点
的边OB上的一点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com