
����Ŀ����֪����������A��B����ʾ�����ֱ�Ϊa��b��������|a��3|��(b��9)2��0��OΪԭ�㣻

(1) a�� ��b�� .
(2) ����C��O����������˶�������3����C��A��ľ�����ڵ�C��B����룬���C���˶��ٶȣ���������ᣬ���з���.��
(3) ����D��2����λÿ����ٶȴӵ�O�����˶���ͬʱ��P�ӵ�A������3����λÿ����ٶ������˶�����Q�ӵ�B��������6����λÿ����ٶ������˶������˶������У�M��N�ֱ�ΪPD��OQ���е㣬��![]() ��ֵ�Ƿ����仯����˵������.��ע��PDָ���ǵ�P��D֮����߶Σ�����ʽPQ��ODָ�߶�PQ��OD���ȵIJ�.���Ƶģ�������������д��ĸд��һ��ʱ����һ����.
��ֵ�Ƿ����仯����˵������.��ע��PDָ���ǵ�P��D֮����߶Σ�����ʽPQ��ODָ�߶�PQ��OD���ȵIJ�.���Ƶģ�������������д��ĸд��һ��ʱ����һ����.
���𰸡���1��-3��9����2����C���ٶ�Ϊÿ��1����λ���ȣ���3��![]() ��ֵû�з����仯�����ɼ�����.
��ֵû�з����仯�����ɼ�����.
��������
��1�����ݼ����Ǹ����ĺ�Ϊ0����ÿһ��������0����������a��b�ķ��̼������a��b��ֵ����2�����ݵ�C��O����������˶�������3����C��A��ľ�����ڵ�C��B����룬�ɱ�ʾ![]() ��
��![]() ������CA=CB��������x�ķ�����⼴�ɣ���3�����ݵ���˶��ٶȺͷ��ֱ��ú�t�Ĵ���ʽ��ʾ��D��P��Q��M��N��Ӧ�������ٷֱ����PQ��OD��MN�ij���Ȼ�����
������CA=CB��������x�ķ�����⼴�ɣ���3�����ݵ���˶��ٶȺͷ��ֱ��ú�t�Ĵ���ʽ��ʾ��D��P��Q��M��N��Ӧ�������ٷֱ����PQ��OD��MN�ij���Ȼ�����![]() ��ֵΪ���������ɵó�����.
��ֵΪ���������ɵó�����.
��1����|a��3|��(b��9)2��0��
��a+3=0��b-9=0�����a=-3��b=9��
��2����3����C��Ӧ����Ϊx��
��![]() ��
��![]() ��
��
��CA=CB����![]() ��
��
��![]() ���⣻
���⣻
��![]() �����x=3����ʱ��C���ٶ�Ϊ3��3=1����λÿ�룬
�����x=3����ʱ��C���ٶ�Ϊ3��3=1����λÿ�룬
���C���ٶ�Ϊÿ��1����λ���ȣ�
��3��![]() ��ֵû�з����仯���������£����˶�ʱ��Ϊt�룬
��ֵû�з����仯���������£����˶�ʱ��Ϊt�룬
���D��Ӧ����Ϊ2t��
��P��Ӧ����Ϊ-3-3t��
��Q��Ӧ����Ϊ9+6t��
��M��Ӧ����Ϊ-1.5-0.5t��
��N��Ӧ����Ϊ4.5+3t��
��PQ=9t+12��OD=2t��MN=3.5t+6��
��![]() ��Ϊ��ֵ��
��Ϊ��ֵ��
��![]() ��ֵû�з����仯.
��ֵû�з����仯.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��b����С������������a��b����![]() ��
��![]() ��0����ش����⣺
��0����ش����⣺
��1����ֱ��д��a��b��c��ֵ��
��2��������a��b��c����Ӧ�ĵ�ֱ�ΪA��B��C����M��A��B֮���һ�����㣬���Ӧ����Ϊm���뻯��![]() ����д��������̣���
����д��������̣���
��3���ڣ�1����2���������£���A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶�������t���ӹ�������B���C֮��ľ����ʾΪBC����A���B֮��ľ����ʾΪAB�����ʣ�BC��AB��ֵ�Ƿ�����ʱ��t�ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˱���������ij�������ۺ�����ָ�Ӳ���������A��B�����ͺŵ���ˮ�����豸��10̨����֪��90��Ԫ����A�ͺŵ���ˮ�����豸��̨������75��Ԫ����B�ͺŵ���ˮ�����豸��̨����ͬ��ÿ̨�豸�۸��´�����ˮ�����±���ʾ��
��ˮ�����豸 | A�� | B�� |
�۸���Ԫ/̨�� | m | m-3 |
�´�����ˮ������/̨�� | 220 | 180 |
��1����m��ֵ��
��2���������ʽ����ƣ�ָ�Ӳ����ڹ�����ˮ�����豸���ʽ���165��Ԫ�����ж����ֹ����������ÿ����ദ����ˮ���Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�OΪԭ�㣬��A��1��0������B��0�� ![]() �����ѡ�ABO�Ƶ�O˳ʱ����ת����A��B��O������ת��Ϊ����
�����ѡ�ABO�Ƶ�O˳ʱ����ת����A��B��O������ת��Ϊ����
��������ͼ�٣�����=30��ʱ�����B�������ꣻ
��������ֱ��AA����ֱ��BB���ཻ�ڵ�M��
��ͼ�ڣ�����=90��ʱ�����M�����ꣻ
�ڵ�C����1��0�������߶�CM���ȵ���Сֵ����ֱ��д��������ɣ�
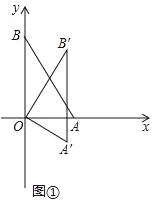
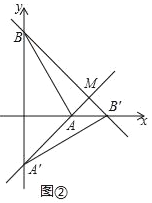
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���A=90������һ�����Ϊ60����BC=6������P��ֱ��AC�ϣ������A��C�غϣ�������ABP=30������CP�ij�Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���BCΪֱ���ġ�O��AB�ڵ�D��AEƽ�֡�BAC��BC�ڵ�E����CD�ڵ�F����CE=CF��
��1����֤��ֱ��CA�ǡ�O�����ߣ�
��2����BD=![]() DC����
DC����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90�㣬����C��ֱ��MN��AB��DΪAB����һ�㣬����D��DE��BC����ֱ��MN��E������ΪF������CD��BE��
��1����֤��CE��AD��
��2����D��AB�е�ʱ���ı���BECD��ʲô�����ı��Σ�˵��������ɣ�
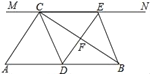
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ����У���ƻ������Ϊ1800m2����������̻������żס����������̶����.��֪��ÿ��������̻���������Ҷ�ÿ��������̻��������2���������ڶ���������Ϊ400 m2������̻�ʱ���ӱ��Ҷ�����4��.
��1����ס��������̶�ÿ��������̻�������ֱ��Ƕ���m2��
��2����ѧУÿ���踶���ӵ��̻�������0.4��Ԫ���Ҷ�Ϊ0.25��Ԫ��Ҫʹ��ε��̻��ܷ��ò�����8��Ԫ������Ӧ���żӹ��������죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���D��������OABC�ı�AB�ϵĶ��㣬OC��6����ADΪһ����AB���Ҳ���������ADEF������BF��DE��P�㣮
��1����ֱ��д����A��B�����ꣻ
��2���ڵ�D���˶������У�OD��BF�Ƿ���������λ�ù�ϵ�������ڣ���д��OD��BF��λ�ù�ϵ����֤�����������ڣ���˵�����ɣ�
��3����P��Ϊ�߶�DE�����ȷֵ�ʱ�������AF�ij��ȣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com