
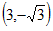 .
.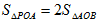 ;
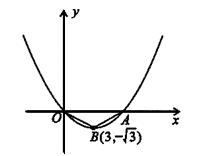
;
解:(1 )∵抛物线的顶点为B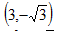
∴设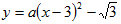
抛物线经过原点(0、0)
∴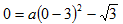
∴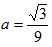
∴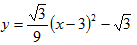 ,即
,即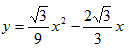
令y=0得: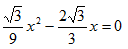
解得x1=0,x2=6,∴A的坐标为(6,0)
(2)∵△AOB与△POA同底不同高,且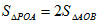
∴△POA中OA边上的高是△AOB中OA边上高的2倍
即P 点纵坐标是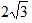
∴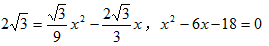
解得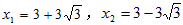
∴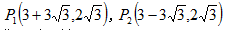
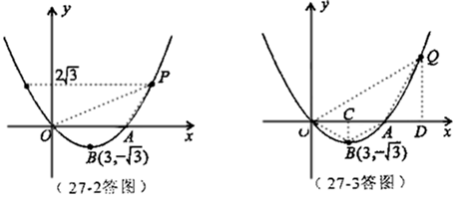
(3)过B作BC⊥轴于C
在Rt△OBC中,tan∠OBC=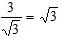
∴∠OBC=60°,而OB=AB,故∠OBA=120°
分两种情况:当点Q在x轴下方时,△QAO就是△BAO,
此时Q点坐标Q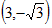
当点Q在轴上方时,由△ABO∽△QAO,有AQ=OA=6,∠OAQ=120°,
作QD⊥x轴,,垂足为D,则∠QAD=60°,∴QD=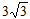 ,AD=3,
,AD=3,
∴OD=9.
此时Q点坐标是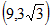
而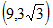 满足关系
满足关系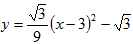 ,即Q在抛物线上
,即Q在抛物线上
根据对称性可知点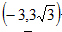 也满足条件
也满足条件
∴Q点坐标为Q1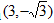 ,Q2
,Q2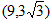 ,Q3
,Q3


科目:初中数学 来源: 题型:
 与x轴的另一个交点为E.
与x轴的另一个交点为E.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| c | a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com