
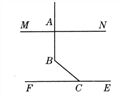
【题目】如图,已知MN⊥AB,∠ABC=130°,∠FCB=40°,试判断直线MN与EF的位置关系,并说明理由.(至少用两种方法说明)
【答案】见解析
【解析】试题分析:MN∥EF, 方法一:延长AB交EF于点D,通过三角形内角和求得∠BDC=90°再由已知求得∠1=90°,从而得∠1=∠BDC,从而得证;
方法二:过点B作直线PQ∥EF, 由已知可证明MN∥PQ,从而得证.
试题解析:MN∥EF,理由如下:
方法一:如图,延长AB交EF于点D,
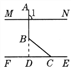
∵∠ABC=130°,∴∠DBC=180°-130°=50°,
∵∠FCB=40°,∠BDC+∠CBD+∠FCB=180°,
∴∠BDC=90°,∵MN⊥AB,∴∠1=90°,
∴∠1=∠BDC,∴MN∥EF;
方法二:过点B作直线PQ∥EF,如图所示,
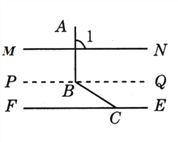
∵PQ∥EF,∴∠CBQ=∠FCB=40°,
∵∠ABC=130°,∴∠ABQ=90°,
∵MN⊥AB,∴∠1=90°,
∴∠1=∠ABQ,∴MN∥PQ,
又∵PQ∥EF,∴MN∥EF.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】根据图形填空:

(1)若直线ED,BC被直线AB所截,则∠1和__________是同位角.
(2)若直线ED,BC被直线AF所截,则∠3和__________是内错角.
(3)∠1和∠3是直线AB,AF被直线__________所截构成的__________角.
(4)∠2和∠4是直线__________,__________被直线BC所截构成的__________角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,抛物线![]() 与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为
与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为![]() .
.
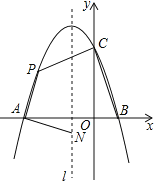
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变量之间关系中,一个变量是另一个变量的正比例函数的是( )
A.正方形的面积S随着边长x的变化而变化
B.正方形的周长C随着边长x的变化而变化
C.水箱有水10L,以0.5L/min的流量往外放水,水箱中的剩水量V(L)随着放水时间t(min)的变化而变化
D.面积为20的三角形的一边a随着这边上的高h的变化而变化
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com