【题目】如图，在
中，
，
于
，将
沿
折叠为
，将
沿
折叠为
，延长
和
相交于点
．
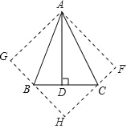
（1）求证：四边形
为正方形；
（2）若
，
，求的长．
【答案】（1）见解析；（2）
【解析】
（1）由折叠的性质可得到的条件是：①AG=AD=AF，②∠GAF=∠GAD+∠DAF=2∠BAC=90°，且∠G=∠F=90°；由②可判定四边形AGHF是矩形，由AG=AF可证得四边形AGHF是正方形；
（2）设AD=x，由折叠的性质可得：AD=AF=x（即正方形的边长为x），BG=BD=6，CF=CD=4；进而可用x表示出BH、HC的长，即可在Rt△BHC中，由勾股定理求得AD的长，进而可求出AB的长．
解：（1）
，
；
由折叠可知，
，
，
，
，
；
；
四边形
是正方形，
（2）
四边形是正方形，
，
又
，
，
；
设
的长为
，则
，
．
在
中，
，
，
解得
，
（不合题意，舍去），
，
．
科目：初中数学 来源： 题型：
【题目】抛物线y=﹣x2+bx+c经过点A、B、C，已知A（﹣1，0），C（0，3）．
（1）求抛物线的解析式；
（2）如图1，P为线段BC上一点，过点P作y轴平行线，交抛物线于点D，当△BDC的面积最大时，求点P的坐标；
（3）如图2，抛物线顶点为E，EF⊥x轴于F点，M（m，0）是x轴上一动点，N是线段EF上一点，若∠MNC=90°，请指出实数m的变化范围，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的一元二次方程x2－2
x＋m＝0有两个不相等的实数根．
(1)求实数m的最大整数值；
(2)在(1)的条件下，方程的实数根是x1，x2，求代数式
＋
－
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，A（4，3）是反比例函数y=
在第一象限图象上一点，连接OA，过A作AB∥x轴，截取AB=OA（B在A右侧），连接OB，交反比例函数y=的图象于点P．
（1）求反比例函数y=的表达式；
（2）求点B的坐标；
（3）求△OAP的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，反比例函数y= 
的图象与一次函数y=x+b的图象交
于点A（1，4）、点B（-4，n）．
（1）求一次函数和反比例函数的解析式；
（2）求△OAB的面积；
（3）直接写出一次函数值大于反比例函数值的自变量x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
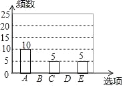
【题目】王老师为了解同学们对金庸武侠小说的阅读情况，随机对初三年级的部分同学进行调查，将调查结果分成以下五类：A：看过0～3本，B：看过4～6本，C：看过7～9本，D：看过10～12本，E：看过13～15本.并根据调查结果绘制了如图1、图2两幅不完整的统计图．
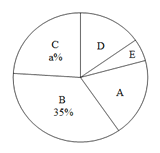
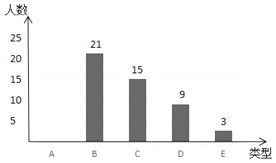
(1)图2中的a = ，D所对的圆心角度数为 °；
(2)请补全条形统计图；
(3)本次调查中E类有2男1女，王老师想从中抽取2名同学分别撰写一篇读书笔记．请用列表或画树状图的方法求所抽取的两名学生恰好是一男一女的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着移动终端设备的升级换代，手机己经成为我们生活中不可缺少的一部分，为了解中学生在假期使用手机的情况（选项：A．和同学亲友聊天：B．学习：C．购物：D．游戏：E．其他），端午节后某中学在全校范围内随机抽取了若干名学生进行调查，得到如下图表（部分信息未给出）：
选项 | 频数 | 百分比 |
A | 10 | m |
B | n | 20% |
C | 5 | 10% |
D | p | 40% |
E | 5 | 10% |
合计 | 100% |
根据以上信息解答下列问题：
（1）m＝ ，n＝ ，p＝ ；
（2）补全条形统计图；
（3）若该中学约有800名学生，估计全校学生中利用手机购物或玩游戏的共有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明大学毕业回家乡创业，第一期培植盆景与花卉各50盆售后统计，盆景的平均每盆利润是160元，花卉的平均每盆利润是19元，调研发现：
①盆景每增加1盆，盆景的平均每盆利润减少2元;每减少1盆，盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆，设培植的盆景比第一期增加x盆，第二期盆景与花卉售完后的利润分别为W1，W2（单位：元）
（1）用含x的代数式分别表示W1，W2;
（2）当x取何值时，第二期培植的盆景与花卉售完后获得的总利润W最大，最大总利润是多少?
查看答案和解析>>
科目：初中数学 来源： 题型：
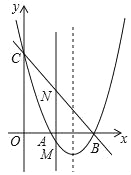
【题目】如图，抛物线y=x2+bx+c与x轴交于点A和B（3，0），与y轴交于点C（0，3）．
（1）求抛物线的解析式；
（2）若点M是抛物线上在x轴下方的动点，过M作MN∥y轴交直线BC于点N，求线段MN的最大值；
（3）E是抛物线对称轴上一点，F是抛物线上一点，是否存在以A，B，E，F为顶点的四边形是平行四边形？若存在，请直接写出点F的坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com