
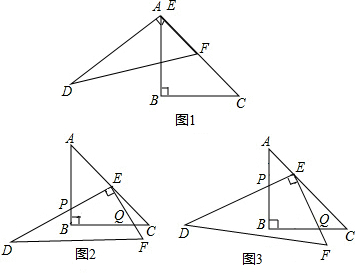
分析 (1)连接BE,根据已知条件得到E是AC的中点,根据等腰直角三角形的性质可以证明DE=CE,∠PBE=∠C.根据等角的余角相等可以证明∠BEP=∠CEQ.即可得到全等三角形,从而证明结论;
(2)作EM⊥AB,EN⊥BC于M、N,根据两个角对应相等证明∴△EMQ∽△ENP,再根据等腰直角三角形的性质得到EM:EN=EQ:EP;
(3)根据(2)中求解的过程,可以直接写出结果;要求m的取值范围,根据交点的位置的限制进行分析.
解答 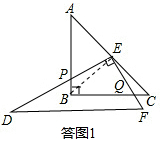 (1)EP=EQ,
(1)EP=EQ,
证明:连接BE,如答图1,
根据E是AC的中点和等腰直角三角形的性质,得:BE=CE,∠PBE=∠C=45°,
∵∠BEC=∠FED=90°
∴∠BEP=∠CEQ,
在△BEP和△CEQ中
$\left\{\begin{array}{l}{∠BEP=∠CEQ}\\{BE=CE}\\{∠PBE=∠C}\end{array}\right.$,
∴△BEP≌△CEQ(ASA),
∴EP=EQ.
故答案是:EP=EQ;
(2)EQ=2EP.
理由:过E作EM⊥BC于M,过E作EN⊥AB于N,如答图2,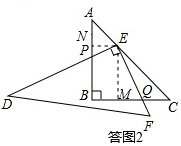
则EM=$\frac{{\sqrt{2}}}{2}$EC,EN=$\frac{{\sqrt{2}}}{2}$AE
∵$\frac{CE}{EA}=2$
∴$\frac{EM}{EN}=2$.
∵∠MQE+∠MEP=∠NPE+∠MEP=90°
∴∠MQE=∠NPE.
又∠EMQ=∠ENP
∴△EMQ∽△ENP
∴$\frac{EQ}{EP}=\frac{EM}{EN}=2$
即:EQ=2EP;
(3)如答图2,∵在四边形PEQB中,∠B=∠PEQ=90°,
∴∠EPB+∠EQB=180°,
又∵∠EPB+∠NPE=180°,
∴∠NPE=∠EQM,
∴Rt△NEP∽Rt△MEQ,
∴$\frac{EP}{EQ}$=$\frac{NE}{EM}$,
Rt△ANE∽Rt△EMC,
∴$\frac{CE}{EA}$=m=$\frac{EM}{NE}$,
∴$\frac{EP}{EQ}$=1:m=$\frac{AE}{CE}$,
EP与EQ满足的数量关系式1:m,即EQ=mEP,
∴0≤m≤2+$\sqrt{6}$,(因为当m>2+$\sqrt{6}$时,EF和BC变成不相交).
故答案是:EQ=mEP.
点评 本题考查了几何变换综合题,涉及了等腰直角三角形的性质、全等三角形的判定与性质、相似三角形的判定与性质,综合考察的知识点较多,对于此类综合性较强的题目,关键还是需要同学们有扎实的基本功,注意培养自己的融会贯通能力.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,小华在∠AOB的内部取一点P,过点P作PE⊥OA,PF⊥OB,垂足分别为点E,F,量得PE=PF;又在边OA,OB上分别取点C,D,使OC=OD,连接PC,PD.于是,她得出结论PC=PD,你认为她的结论正确吗?请说明理由.
如图,小华在∠AOB的内部取一点P,过点P作PE⊥OA,PF⊥OB,垂足分别为点E,F,量得PE=PF;又在边OA,OB上分别取点C,D,使OC=OD,连接PC,PD.于是,她得出结论PC=PD,你认为她的结论正确吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
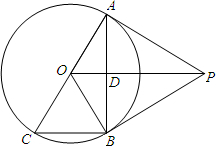 如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,AB是弦,PA∥BC交AB于点D
如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,AB是弦,PA∥BC交AB于点D查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,BC=6cm,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形.求:
如图,在平行四边形ABCD中,BC=6cm,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
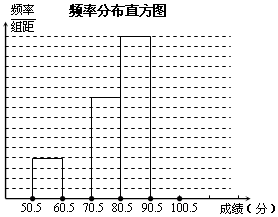 为了让学生了解环保知识,增强环保意识.某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识.某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 008 |
| 60.5~70.5 | 8 | b |
| 70.5~80.5 | 10 | 020 |
| 80.5~90.5 | 16 | 032 |
| 90.5~100.5 | a | 0.24 |
| 合计 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
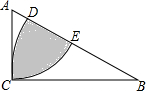 如图,在Rt△ABC中,∠A=60°,AB=2,以点B为圆心,BC为半径的弧交AB于点D,以点A为圆心,AC为半径的弧交AB于点E,则图中阴影部分的面积为$\frac{5π-6\sqrt{3}}{12}$.
如图,在Rt△ABC中,∠A=60°,AB=2,以点B为圆心,BC为半径的弧交AB于点D,以点A为圆心,AC为半径的弧交AB于点E,则图中阴影部分的面积为$\frac{5π-6\sqrt{3}}{12}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
如图,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com