
 如图,在Rt△AOD中,∠AOD=90°,点 B,C在OD上,且OA=OB=BC=CD.求证:△ABC∽△DBA.
如图,在Rt△AOD中,∠AOD=90°,点 B,C在OD上,且OA=OB=BC=CD.求证:△ABC∽△DBA. 分析 根据已知及相似三角形的判定进行分析,从而得到答案.
解答 证明:∵∠AOD=90°,设OA=OB=BC=CD=x
∴AB=$\sqrt{2}$x,AC=$\sqrt{5}$x,AD=$\sqrt{10}$x,OC=2x,OD=3x,BD=2x
∴$\frac{AB}{BD}$=$\frac{\sqrt{2}x}{2x}$=$\frac{\sqrt{2}}{2}$,$\frac{BC}{AB}$=$\frac{x}{\sqrt{2}x}$=$\frac{\sqrt{2}}{2}$,$\frac{AC}{DA}$=$\frac{\sqrt{5}x}{\sqrt{10}x}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{AB}{BD}$=$\frac{BC}{AB}$=$\frac{AC}{DA}$,
∴△ABC∽△DBA.
点评 此题考查了相似三角形的判定:①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 2m2-1 | B. | 2n2-mn+1 | C. | 2n2-mn-1 | D. | mn-2n2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知等边△ABC,请做出旋转后的三角形.
已知等边△ABC,请做出旋转后的三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
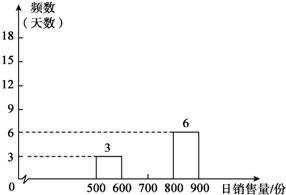 夏季来临,某饮品店老板大白计划下个月(2015年8月)每天制作新鲜水果冰淇淋800份销售.去年同期,这种冰淇淋每份的成本价为5元,售价为8元.该冰淇淋不含防腐剂,很受顾客的欢迎,但如果当天制作的冰淇淋未售出,新鲜水果就会腐败变质,饮品店就将承担冰淇淋制作成本的损失.根据大白去年的销售记录,得到去年同期该冰淇淋日销售量的频数分布表和频数分布直方图(不完整)如下:
夏季来临,某饮品店老板大白计划下个月(2015年8月)每天制作新鲜水果冰淇淋800份销售.去年同期,这种冰淇淋每份的成本价为5元,售价为8元.该冰淇淋不含防腐剂,很受顾客的欢迎,但如果当天制作的冰淇淋未售出,新鲜水果就会腐败变质,饮品店就将承担冰淇淋制作成本的损失.根据大白去年的销售记录,得到去年同期该冰淇淋日销售量的频数分布表和频数分布直方图(不完整)如下:| 日销售量分组 | 频数 |
| 500≤x<600 | 3 |
| 600≤x<700 | 6 |
| 700≤x<800 | 16 |
| 800≤x<900 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com