根据所给的基本材料，请你进行适当的处理，编写一道综合题．
编写要求：①提出具有综合性、连续性的三个问题；②给出正确的解答过程；③写出编写意图和学生答题情况的预测．
材料①：如图，先把一矩形纸片ABCD对折，得到折痕MN，然后把B点叠在折痕线上，得到△ABE，再过点B把矩形ABCD第三次折叠，使点D落在直线AD上，得到折痕PQ．当沿着BE第四次将该纸片折叠后，点A就会落在EC上．
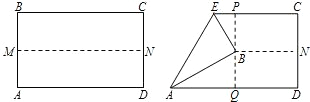
材料②：已知AC是∠MAN的平分线．
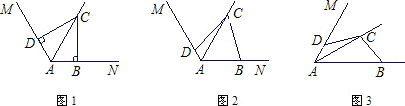
（1）在图1中，若∠MAN=120°，∠ABC=ADC=90°，求证：AB+AD=AC；
（2）在图2中，若∠MAN=120°，∠ABC+∠ADC=180°，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；
（3）在图3中：若∠MAN=α（0°＜α＜180°），∠ABC+∠ADC=180°，
则AB+AD=
AC（用含α的三角函数表示）．
材料③：
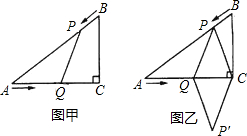
已知：如图甲，在Rt△ACB中，∠C=90°，AC=4cm，BC=3cm，点P由B出发沿线段BA向点A匀速运动，速度为1cm/s；点Q由A出发沿线段AC向点C匀速运动，速度为2cm/s；连接PQ，设运动的时间为t（s）（0＜t＜2）．
编写试题选取的材料是
（填写材料的序号）
编写的试题是：（1）设△AQP的面积为y（cm
2），求y与t之间的函数关系式．
（2）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值．
（3）如图（2），连接PC，并把△PQC沿QC翻折得到四边形PQP'C．是否存在某一时刻t，使四边形PQP'C为菱形？若存在，求出此时菱形的边长．
试题解答（写出主要步骤即可）：（1）过点Q作QD⊥AP于点D，证△AQD∽△ABC，利用相似性质及面积解答；
（2）分别求得Rt△ACB的周长和面积，由周长求出t，代入函数解析式验证；
（3）利用余弦定理得出PC、PQ，联立方程，求得t，再代入PC解得答案．
计算高手系列答案
在矩形ABCD中，AB=6cm，BC=8cm，若将矩形对角线BD对折，使B点与D点重合，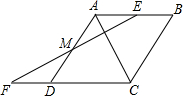
如图，四边形ABCD是菱形，过AB的中点E作AC的垂线EF，交AD于点M，交CD的延长线于点F．
，求
的度数。 