
【题目】如图,在线段BC上有两点E,F,在线段CB的异侧有两点A,D,满足AB=CD,AE=DF,CE=BF,连接AF;
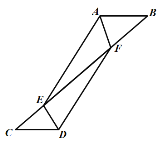
(1)连接DE,求证:四边形AEDF是平行四边形;
(2)若∠B=40°,∠DFC=30°,当AF平分∠BAE时,求∠BAF.
【答案】(1)见解析 (2)55°
【解析】
(1)先证明△ABE≌△DCF,进而证得AE∥DF,再结合AE=DF即可证明;
(2)由△ABE≌△DCF,可得∠AEB=∠DFC=30°,然后由三角形内角和定理可得∠BAE=110°,最后根据角平分线的性质解答即可.
(1)证明:∵CE=BF,
∴CE+EF=BF+EF,
∴BE=CF,
在△ABE和△DCF中,
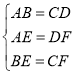 ,
,
∴△ABE≌△DCF(SSS),
∴∠BEA=∠CFD;
∴AE∥DF,
又∵AE=DF,
∴四边形AEDF是平行四边形
(2)解:由(1)得:△ABE≌△DCF,
∴∠AEB=∠DFC=30°,
∴∠BAE=180°﹣∠B﹣∠AEB=180°﹣40°﹣30°=110°,
∵AF平分∠BAE,
∴∠BAF=![]() ∠BAE=
∠BAE=![]() ×110°=55°
×110°=55°


科目:初中数学 来源: 题型:
【题目】初中生对待学习的态度一直是教育工作者关注的问题之一,为此蓬溪县教体局教研室对我县部分学校的九年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
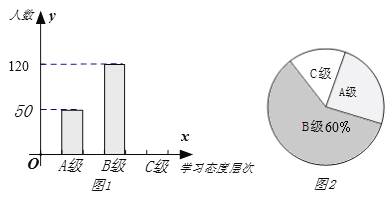
(1)此次抽样调查中,共调查了______名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查的结果,请你估计我县初三6000名学生中有多少名学生学习态度达标(达标包括A级和B级)?
查看答案和解析>>
科目:初中数学 来源: 题型:
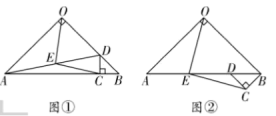
【题目】如图①,在![]() 中,
中,![]() 为
为![]() 边上一点,过
边上一点,过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(观察猜想)
(1)①![]() 的数量关系是___________
的数量关系是___________
②![]() 的数量关系是______________
的数量关系是______________
(类比探究)
(2)将图①中![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(拓展迁移)
(3)将![]() 绕点
绕点![]() 旋转任意角度,若
旋转任意角度,若![]() ,请直接写出点
,请直接写出点![]() 在同一直线上时
在同一直线上时![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
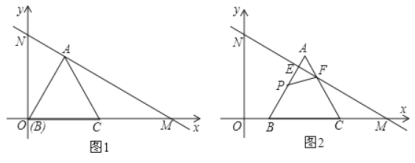
【题目】如1,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,等边
,等边![]() 的顶点
的顶点![]() 与原点
与原点![]() 重合,
重合,![]() 边落在
边落在![]() 轴正半轴上,点
轴正半轴上,点![]() 恰好落在线段
恰好落在线段![]() 上,将等边
上,将等边![]() 从图1的位置沿
从图1的位置沿![]() 轴正方向以每秒1个单位长度的速度平移,边
轴正方向以每秒1个单位长度的速度平移,边![]() 分别与线段
分别与线段![]() 交于点
交于点![]() (如图2所示),设
(如图2所示),设![]() 平移的时间为
平移的时间为![]() (s).
(s).
(1)![]() ,等边
,等边![]() 的边长为 ;
的边长为 ;
(2)在运动过程中,当![]() 为何值时,MN垂直平分AB;
为何值时,MN垂直平分AB;
(3)在![]() 开始平移的同时,点
开始平移的同时,点![]() 从
从![]() 的顶点
的顶点![]() 出发,以每秒2个单位长度的速度沿折线
出发,以每秒2个单位长度的速度沿折线![]() 运动,当点
运动,当点![]() 运动到
运动到![]() 时立即停止运动,
时立即停止运动,![]() 也随之停止平移.
也随之停止平移.
①当点![]() 在线段
在线段![]() 上运动时,若
上运动时,若![]() ,求
,求![]() 的值;
的值;
②当点![]() 在线段
在线段![]() 上运动时,若
上运动时,若![]() 的面积
的面积![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,圆内接四边形ABCD,AD=BC,AB是⊙O的直径.
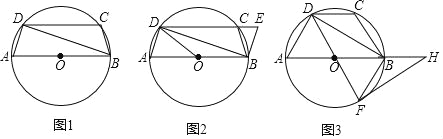
(1)求证:AB∥CD;
(2)如图2,连接OD,作∠CBE=2∠ABD,BE交DC的延长线于点E,若AB=6,AD=2,求CE的长;
(3)如图3,延长OB使得BH=OB,DF是⊙O的直径,连接FH,若BD=FH,求证:FH是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
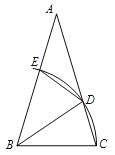
【题目】如图,已知△ABC中,∠ABC=∠ACB,以点B为圆心,BC长为半径的弧分别交AC,AB于点D,E,连接BD,ED.
(1)写出图中所有的等腰三角形;
(2)若∠AED=114°,求∠ABD和∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学课外活动中,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向,办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(结果精确到0.1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年初,新冠肺炎肆虐全球.我国政府和人民采取了积极有效的防疫措施,疫情在我国得到了有效控制.小明为复学到药店购买![]() 口罩和一次性医用口罩.已知购买
口罩和一次性医用口罩.已知购买![]() 个
个![]() 口罩和
口罩和![]() 个一次性医用口罩共需
个一次性医用口罩共需![]() 元;购买
元;购买![]() 个
个![]() 口罩和
口罩和![]() 个一次性医用罩共需
个一次性医用罩共需![]() 元.
元.
(1)求![]() 口罩与一次性医用口罩的单价;
口罩与一次性医用口罩的单价;
(2)小明准备购买![]() 口罩和一次性医用口罩共
口罩和一次性医用口罩共![]() 个,且
个,且![]() 口罩的数量不少于一次性医用口罩数量的
口罩的数量不少于一次性医用口罩数量的![]() .请设计出最省钱的购买方案,并说明理由.
.请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com