
 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
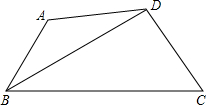 如图,四边形ABCD中,∠A+∠C=180°,BD平分∠ABC,
如图,四边形ABCD中,∠A+∠C=180°,BD平分∠ABC,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
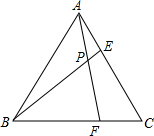 如图,等边△ABC的边长是6,点E,F分别在AC,BC边上,AE=CF,连接AF,BE相交于点P.
如图,等边△ABC的边长是6,点E,F分别在AC,BC边上,AE=CF,连接AF,BE相交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
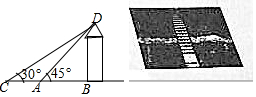 崇圣寺三塔位于大理古城西北部1.5公里处,它是大理历史上规模最为宏大的古刹,南迢丰佑年间曾有殿宇千间,大理国时期是皇家的寺院,崇圣寺三塔由一大二小三阁组成,大塔又名千寻塔.当地群众称它为“文笔塔”,某校数学兴趣小组的同学欲测量主塔垂直于地面的高度BD,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退50.6m至C处,侧得右塔顶端点D的仰角为30°,求该古塔BD的高度($\sqrt{3}≈1.732$,结果保留两位小数).
崇圣寺三塔位于大理古城西北部1.5公里处,它是大理历史上规模最为宏大的古刹,南迢丰佑年间曾有殿宇千间,大理国时期是皇家的寺院,崇圣寺三塔由一大二小三阁组成,大塔又名千寻塔.当地群众称它为“文笔塔”,某校数学兴趣小组的同学欲测量主塔垂直于地面的高度BD,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退50.6m至C处,侧得右塔顶端点D的仰角为30°,求该古塔BD的高度($\sqrt{3}≈1.732$,结果保留两位小数).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com