
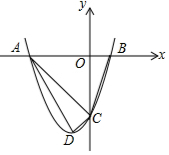
 已知:二次函数y=mx2+2mx-3m的图象与x轴交于A、B两点(点A在左,点B在右),与y轴交于点C(m>0),顶点为D.当m取何值时,以A、D、C三点为顶点的三角形与△OBC相似?
已知:二次函数y=mx2+2mx-3m的图象与x轴交于A、B两点(点A在左,点B在右),与y轴交于点C(m>0),顶点为D.当m取何值时,以A、D、C三点为顶点的三角形与△OBC相似? 分析 分两种情形讨论即可:①当∠ACD=90°时,作DH⊥OC于H.由△AOC∽△CHD,推出$\frac{OA}{CH}$=$\frac{OC}{DH}$,可得$\frac{3}{m}$=$\frac{3m}{1}$,解得m=1或-1(舍弃),由此即可判断.②当∠ADC=90°时,作DH⊥OC于H,AE⊥DH于E.由△AED∽△DHC,可得$\frac{AE}{DH}$=$\frac{DE}{CH}$,可得$\frac{4m}{1}$=$\frac{2}{m}$,求得m=$\frac{\sqrt{2}}{2}$或-$\frac{\sqrt{2}}{2}$(舍弃),由此即可解决问题.
解答 解:①当∠ACD=90°时,作DH⊥OC于H.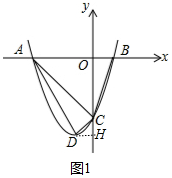
由题意可知A(-3,0),B(1,0),C(0,-3m),D(-1,-4m),
∵∠ACO+∠CAO=90°,∠ACO+∠DCH=90°,
∴∠CAO=∠DCH,∵∠AOC=∠DHC=90°,
∴△AOC∽△CHD,
∴$\frac{OA}{CH}$=$\frac{OC}{DH}$,
∴$\frac{3}{m}$=$\frac{3m}{1}$,
∴m=1或-1(舍弃),
∴C(0,-3),D(-1,-4),
∴OA=3$\sqrt{2}$,CD=$\sqrt{2}$,
∴$\frac{AC}{CD}$=$\frac{OC}{OB}$=3,
∴$\frac{AC}{OC}$=$\frac{CD}{OB}$,∵∠ACD=∠BOC=90°,
∴△BOC∽△DCA.
②当∠ADC=90°时,作DH⊥OC于H,AE⊥DH于E.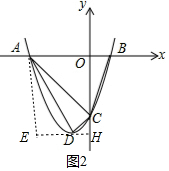
由△AED∽△DHC,可得$\frac{AE}{DH}$=$\frac{DE}{CH}$,
∴$\frac{4m}{1}$=$\frac{2}{m}$,
∴m=$\frac{\sqrt{2}}{2}$或-$\frac{\sqrt{2}}{2}$(舍弃),
∴AE=2$\sqrt{2}$,AD=2$\sqrt{3}$,DC=$\frac{\sqrt{6}}{2}$,
显然此时△ADC与△OBC不相似.
综上所述,m=1时,以A、D、C三点为顶点的三角形与△OBC相似.
点评 本题考查相似三角形的判定和性质、抛物线与坐标轴的交点问题、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会用方程的思想思考问题,属于中考常考题型.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:选择题
| A. | 对学校的同学发放问卷进行调查 | |
| B. | 对在路边行走的学生随机发放问卷进行调查 | |
| C. | 对在图书馆里看书的人发放问卷进行调查 | |
| D. | 对在路边行走的路人随机发放问卷进行调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
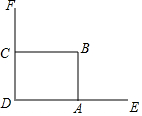 某县扶贫开发办公室为帮助该县贫困户开发经济、发展生产、特为贫困户建设养鸡舍及围栏.在为某农户修建鸡舍时,该农户想借助如图所示的直角旧墙角,用22米长的围栏(全部用完)围成一个矩形鸡舍ABCD,点C在墙DF(墙DF的长为11米)上,点A在墙DE(墙DE足够长)上.(围栏只围AB,BC两边)
某县扶贫开发办公室为帮助该县贫困户开发经济、发展生产、特为贫困户建设养鸡舍及围栏.在为某农户修建鸡舍时,该农户想借助如图所示的直角旧墙角,用22米长的围栏(全部用完)围成一个矩形鸡舍ABCD,点C在墙DF(墙DF的长为11米)上,点A在墙DE(墙DE足够长)上.(围栏只围AB,BC两边)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1°C | B. | 0°C | C. | 1°C | D. | -2°C |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 45.5°=45°30′ | B. | 3a+b=3ab | C. | -$\frac{1}{2}$>-$\frac{1}{3}$ | D. | a3+a2=a5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 任意抛掷一枚图钉,结果针尖朝上 | |
| B. | 任意抛掷一枚均匀的骰子,骰子停止转动后,朝上的一面的点数为1 | |
| C. | 连结⊙O的一条弦的中点和圆心的直线垂直这条弦 | |
| D. | 在一张纸上画两个三角形,这两个三角形相似 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com