Question

10．结合数轴与绝对值的知识回答下列问题：

（1）数轴上表示4和1的两点之间的距离是3；表示-3和2两点之间的距离是5；一般地，数轴上表示数m和数n的两点之间的距离等于|m-n|．如果表示数a和-1的两点之间的距离是3，那么a=-4或2．
（2）若数轴上表示数a的点位于-4与2之间，则|a+4|+|a-2|的值为6；
（3）利用数轴找出所有符合条件的整数点x，使得|x+2|+|x-5|=7，这些点表示的数的和是12．
（4）当a=1时，|a+3|+|a-1|+|a-4|的值最小，最小值是7．

Answer 1

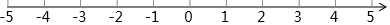
分析 （1）根据数轴，求出两个数的差的绝对值即可；
（2）先去掉绝对值号，然后进行计算即可得解；
根据两点间的距离的表示列式计算即可得解；
（3）找到-2和5之间的整数点，再相加即可求解；
（4）判断出a=1时，三个绝对值的和最小，然后进行计算即可得解．

解答 解：（1）|1-4|=3，
|-3-2|=5，
|a-（-1）|=3，
所以，a+1=3或a+1=-3，
解得a=-4或a=2；

（2）∵表示数a的点位于-4与2之间，
∴a+4＞0，a-2＜0，
∴|a+4|+|a-2|=（a+4）+[-（a-2）]=a+4-a+2=6；

（3）使得|x+2|+|x-5|=7的整数点有-2，-1，0，1，2，3，4，5，
-2-1+0+1+2+3+4+5=12．
故这些点表示的数的和是12；

（4）a=1有最小值，最小值=|1+3|+|1-1|+|1-4|=4+0+3=7．
故答案为：3，5，-4或2；6；12；1；7．

点评 本题考查了绝对值，数轴，读懂题目信息，理解数轴上两个数之间的距离的表示方法是解题的关键．