
【题目】如图,在边长为3cm的正方形ABCD中,点E为BC边上的任意一点,AF⊥AE,AF交CD的延长线于F,则四边形AFCE的面积为cm2 . 
【答案】9
【解析】解:∵四边形ABCD是正方形, ∴AD=AB,∠ADF=∠DAB=∠B=90°,
∴∠BAE+∠DAE=90°,
∵AF⊥AE,
∴∠DAF+∠DAE=90°,
∴∠BAE=∠DAF,
在△BAE和△DAF中,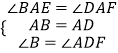 ,
,
∴△BAE≌△DAF(ASA),
∴S△BAE=S△DAF ,
∴S四边形AFCE=S△DAF+S四边形ADCE=S△BAE+S四边形ADCE=S正方形=3×3=9(cm2).
所以答案是:9.
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
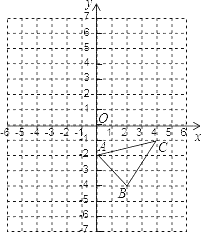
【题目】已知:如图,已知△ABC 中,其中 A(0,﹣2),B(2,﹣4),C(4,﹣1).
(1)画出与△ABC 关于 y 轴对称的图形△A1B1C1;
(2)写出△A1B1C1 各顶点坐标;
(3)求△ABC 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(a2-4a+2)(a2-4a+6)+4进行因式分解的过程:
解:设a2-4a=y,则
原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(a2-4a+4)2.(第四步)
(1)该同学因式分解的结果是否彻底:________(填“彻底”或“不彻底”);
(2)若不彻底,请你直接写出因式分解的最后结果:________;
(3)请你模仿以上方法对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC,△ABC≌△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点,观察并猜想线段EA1与FC有怎样的数量关系?并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如今,网上购物已成为一种新的消费时尚,精品书店想购买一种贺年卡在元旦时销售,在互联网上搜索了甲、乙两家网
店(如图所示),已知两家网店的这种贺年卡的质量相同,请看图回答下列问题:
(1)假若精品书店想购买x张贺年卡,那么在甲、乙两家网店分别需要花多少钱(用含有x的式子表示)?(提示:如需付运费时运费只需付一次,即8元)
(2)精品书店打算购买300张贺年卡,选择哪家网店更省钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有( )
A.∠ADE=20°
B.∠ADE=30°
C.∠ADE=![]() ∠ADC
∠ADC
D.∠ADE=![]() ∠ADC
∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
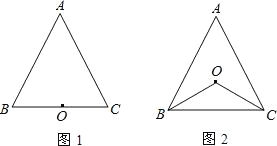
【题目】已知,点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在BC上,求证:△ABC是等腰三角形.
(2)如图2,若点O在△ABC内部,求证:AB=AC.
(3)若点O点在△ABC的外部,△ABC是等腰三角形还成立吗?请画图表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点M、N在边BC上.
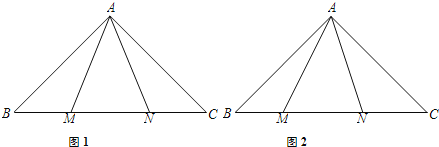
(1)如图1,如果AM=AN,求证:BM=CN;
(2)如图2,如果M、N是边BC上任意两点,并满足∠MAN=45°,那么线段BM、MN、NC是否有可能使等式MN2=BM2+NC2成立?如果成立,请证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E. 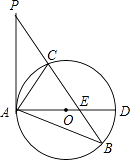
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点C,若ACAB=12,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com