
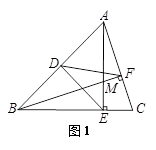
【小题1】问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=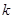 DF,则
DF,则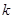 的值为____
的值为____ _.
_. 
【小题2】拓展
问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.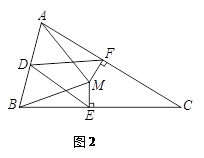
【小题3】推广
问题3 如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证 明你的结论.
明你的结论.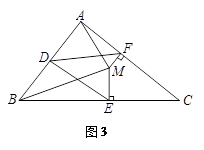
【小题1】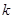 的值为 1
的值为 1
【小题2】证明:如图9.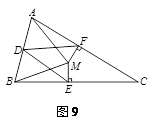
∵CB=CA,
∴∠CAB=∠CBA.
∵∠MAC=∠MBC,
∴∠CAB-∠MAC=∠CBA-∠MBC,
即∠MAB=∠MBA.
∴MA=MB.
∵ME⊥BC,MF⊥AC,垂足分别为点E,F,
∴∠AFM=∠BEM=90°.
在△AFM与△BEM中,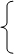 ∠AFM=∠BEM,
∠AFM=∠BEM,
∠MAF =∠MBE, MA=MB,
MA=MB,
∴△AFM≌△BEM.
∵点D是AB边的中点,
∴BD = AD.
在△BDE与△ADF中,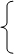 BD = AD,
BD = AD,
∠DBE =∠DAF,
BE = AF,
∴△BDE≌△ADF.
∴DE=DF.
【小题3】解:DE=DF.
证明:分别取AM,BM的中点G,H,连接DG,FG,DH,EH.(如图10)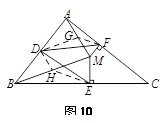
∵点D,G,H分别是AB,AM,BM的中点,
∴DG∥BM,DH∥AM,且DG=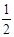 BM,DH=
BM,DH=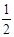 AM.
AM.
∴四边形DHMG是平行四边形.
∴∠DHM =∠DGM,
∵ME⊥BC,MF⊥AC,垂足分别为点E,F,
∴∠AFM=∠BEM=90°.
∴FG=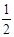 AM= AG,EH=
AM= AG,EH=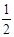 BM= BH
BM= BH .
.
∴FG= DH,DG= EH, ∠GAF =∠GFA,∠HBE =∠HEB.
∴∠FGM =2∠FAM,∠EHM =2∠EBM.
∵∠FAM=∠EBM,
∴∠FGM =∠EHM.
∴∠DGM+∠FGM =∠DHM+∠EHM,即∠DGF=∠DHE.
在△EHD与△DGF中,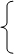 EH = DG,
EH = DG,
∠EHD =∠DGF,
HD = GF,
∴△EHD≌△DGF.
∴DE=DF.
解析


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011年江苏省徐州市初中毕业、升学模拟考试数学卷 题型:解答题
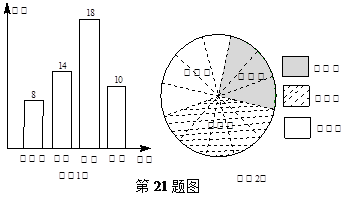
(6分)学生小明、小华到某电脑销售公司参加社会实践活动,了解到2010年该公司经销的甲、己两种品牌电脑在第一季度三个月(即一、二、三月份)的销售数量情况.小明用直方图表示甲品牌电脑在第一季度每个月的销售量的分布情况,见图①;小华用扇形统计图表示乙品牌电脑每个月的销售量与该品牌电脑在第一季度的销售总量的比例分布情况,见图②.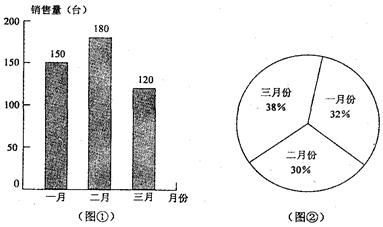
根据上述信息,回答下列问题:
【小题1】 (1)这三个月中,甲品牌电脑在哪个月的销售量最大? ▲ 月份;
【小题2】 (2)已知该公司这三个月中销售乙品牌电脑的总数量比销售甲品牌电脑的总数量多50台,求乙品牌电脑在二月份共销售了多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com