
分析 (1)先计算判别式的值,然后利用△=b2-4ac决定抛物线与x轴的交点的个数可得到结论;
(2)先把A点坐标代入y=x2-(2m-1)x+m2-m中求出m=3或4,然后分别得到m=3和m=4的抛物线解析式,利用抛物线与x轴的交点求出B点坐标,利用y轴上点的坐标特征确定C点坐标,最后根据三角形面积公式求解.
解答 (1)证明:△=(2m-1)2-4(m2-m)
=1>0,
所以此抛物线与x轴必有两个不同的交点;
(2)把A(3,0)代入y=x2-(2m-1)x+m2-m得9-3(2m-1)+m2-m=0,
整理得m2-7m+12=0,解得m1=3,m2=4,
若m=3时,抛物线解析式为y=x2-5x+6,
当y=0时,x2-5x+6=0,解得x1=2,x2=3,则B(2,0);当x=0时,y=x2-5x+6=6,则C(0,6),所以S△ABC=$\frac{1}{2}$×(3-2)×6=3;
若m=4时,抛物线解析式为y=x2-7x+12,
当y=0时,x2-7x+12=0,解得x1=4,x2=3,则B(4,0);当x=0时,y=x2-7x+12=12,则C(0,12),所以S△ABC=$\frac{1}{2}$×(4-3)×12=6.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数.解决此类问题的关键是把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为求方程ax2+bx+c=0的解的问题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
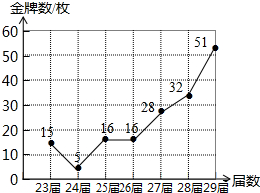 从1984年起,我国先后参加了第23届夏季奥运会,取得了骄人的成绩.如图是根据第23届至29届夏季奥运会我国获得的金牌数绘制的折线统计图,观察统计图可得:与上一届相比增长量最大的是第29届夏季奥运会,比它的上一届增加了19枚金牌.
从1984年起,我国先后参加了第23届夏季奥运会,取得了骄人的成绩.如图是根据第23届至29届夏季奥运会我国获得的金牌数绘制的折线统计图,观察统计图可得:与上一届相比增长量最大的是第29届夏季奥运会,比它的上一届增加了19枚金牌.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com