
在直角坐标系x o y中,已知点P是反比例函数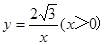 图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.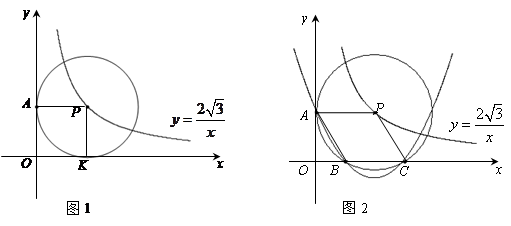
(1)如图1,⊙P运动到与x轴相切时,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:
①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的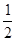 .若存在,请直接写出所有满足条件的M点的坐标,若不存在,试说明理由.
.若存在,请直接写出所有满足条件的M点的坐标,若不存在,试说明理由.
(1)四边形OKPA是正方形 (2)①A(0, ),B(1,0) C(3,0).②满足条件的M的坐标有四个,分别为:(0,
),B(1,0) C(3,0).②满足条件的M的坐标有四个,分别为:(0, ),(3,0),(4,
),(3,0),(4, ),(7,
),(7, )
)
解析试题分析:解:(1)∵⊙P分别与两坐标轴相切,
∴ PA⊥OA,PK⊥OK.
∴∠PAO=∠OKP=90°.
又∵∠AOK=90°,
∴ ∠PAO=∠OKP=∠AOK=90°.
∴四边形OKPA是矩形.
又∵OA=OK,
∴四边形OKPA是正方形.
(2)①连接PB,设点P的横坐标为x,则其纵坐标为 .
.
过点P作PG⊥BC于G.
∵四边形ABCP为菱形,
∴BC=PA=PB=PC.
∴△PBC为等边三角形.
在R t △PBG中,∠PBG=60°,PB=PA=x,
PG= .
.
Sin ∠ PBG= ,即
,即 .
.
解之得:x=±2(负值舍去).
∴ PG= ,PA=BC=2.
,PA=BC=2.
易知四边形OGPA是矩形,PA=OG=2,BG=CG=1,
∴OB=OG-BG=1,OC=OG+GC=3.
∴ A(0, ),B(1,0) C(3,0).
),B(1,0) C(3,0).
设二次函数解析式为:y=ax2+bx+c.
据题意得:
解之得:a= , b=
, b= , c=
, c= .
.
∴二次函数关系式为: .
.
②解法一:设直线BP的解析式为:y="u" x+ v,据题意得:
解之得:u= , v=
, v= .
.
∴直线BP的解析式为: .
.
过点A作直线AM∥PB,则可得直线AM的解析式为: .
.
解方程组:
得: ;
;  .
.
过点C作直线CM∥PB,则可设直线CM的解析式为: .
.
∴0= .
.
∴ .
.
∴直线CM的解析式为: .
.
解方程组:
得: ;
;  .
.
综上可知,满足条件的M的坐标有四个,
分别为:(0, ),(3,0),(4,
),(3,0),(4, ),(7,
),(7, ).
).
解法二:∵ ,
,
∴A(0, ),C(3,0)显然满足条件.
),C(3,0)显然满足条件.
延长AP交抛物线于点M,由抛物线与圆的轴对称性可知,PM=PA.
又∵AM∥BC,
∴ .
.
∴点M的纵坐标为 .
.
又点M的横坐标为AM=PA+PM=2+2=4.
∴点M(4, )符合要求.
)符合要求.
点(7, )的求法同解法一.
)的求法同解法一.
综上可知,满足条件的M的坐标有四个,
分别为:(0, ),(3,0),(4,
),(3,0),(4, ),(7,
),(7, ).
).
解法三:延长AP交抛物线于点M,由抛物线与圆的轴对称性可知,PM=PA.
又∵AM∥BC,
∴ .
.
∴点M的纵坐标为 .
.
即 .
.
解得: (舍),
(舍), .
.
∴点M的坐标为(4, ).
).
点(7, )的求法同解法一.
)的求法同解法一.
综上可知,满足条件的M的坐标有四个,
分别为:(0, ),(3,0),(4,
),(3,0),(4, ),(7,
),(7, ).
).
考点:正方形的性质、二次函数与几何相结合
点评:该题较为复杂,主要考查学生对各种四边形判定的理解和应用,以及对二次函数与几何图形结合所构成的特殊点的联系和求解。


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
 如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=
如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=| k |
| x |
| 75 |
| 16 |
| 75 |
| 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 在直角坐标系中,A(0,4),B(4
在直角坐标系中,A(0,4),B(4| 3 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标系中,半圆直径为OC,其圆心为D.过点A(2,0)作与半圆D相切于点E的切线AB,且∠OAB=45°.
如图,在直角坐标系中,半圆直径为OC,其圆心为D.过点A(2,0)作与半圆D相切于点E的切线AB,且∠OAB=45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com