
【题目】为增强居民节约用水意识,某市在2018年开始对供水范围内的居民用水实行“阶梯收费”,具体收费标准如下表:

某户居民四月份用水10 m3时,缴纳水费23元.
(1) 求a的值;
(2) 若该户居民五月份所缴水费为71元,求该户居民五月份的用水量.
【答案】(1)a的值为2.3;(2)该用户居民五月份的用水量为28 m3.
【解析】
(1)四月份用水10 m3<22 m3,故单价为a元/m.根据“缴纳水费为23元”,列出关于a的方程,即可求出a的值;
(2)当用水量为22 m3时,水费为22×2.3=50.6<71,故五月份用水量超过22 m3;
设五月份用水量为xm3,前22m3的部分,水费为22×2.3,超过22m3的水为(x-22)m3,根据“五月份所缴水费为71元”列出关于x的方程,求出x的值即为五月份用水量.
(1) 由题意,10a=23,解得a=![]() ,即a的值为
,即a的值为![]()
(2) 设用户用水量为x m3,因为用水22 m3时,水费为22×2.3=50.6(元)<71元,
所以x>22,
所以![]()
解得x=28.
答:该用户居民五月份的用水量为28 m3


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
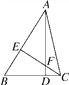
【题目】如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点F.请你添加一个适当的条件,使△AEF≌△CEB.添加的条件是____________(写出一个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y= ![]() x2﹣3x+4,
x2﹣3x+4,
(1)配方成y=a(x﹣h)2+k的形式.
(2)求出它的图象的顶点坐标和对称轴.
(3)求出函数的最大或最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结 合.研究数轴我们发现了许多重要的规律:若数轴上点 A、点 B 表示的数分别为 a、b,则A、B 两点之间的距离 AB= ![]() ,线段 AB 的中点表示的数为
,线段 AB 的中点表示的数为![]() .
.
【问题情境】如图,数轴上点A表示的数为-2,点B表示的数为8,点P从点 A 出发, 以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒 2个单 位长度的速度向左匀速运动,设运动时间为t秒(t>0).
【综合运用】(1) 填空:
①A、B两点之间的距离AB=__________,线段AB的中点表示的数为_______;
②用含t的代数式表示:t秒后,点P表示的数为_______;点Q表示的数为_____.
(2) 求当t为何值时,P、Q 两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点 P在运动过程中,线段MN的长度是否发 生变化?若变化,请说明理由;若不变,请求出线段MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于点B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,若tan∠ABO= ![]() ,OB=4,OE=2,点D的坐标为(6,m).
,OB=4,OE=2,点D的坐标为(6,m). 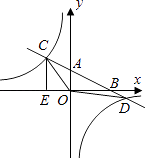
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天下午的营运全是在东西走向的人民大街上进行的.如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 人民大街总长不小于________千米;
人民大街总长不小于________千米;
![]() 将最后一名乘客送往目的地时,小李距离下午出车时的出发点多远?
将最后一名乘客送往目的地时,小李距离下午出车时的出发点多远?
![]() 若出租车耗油量为每千米
若出租车耗油量为每千米![]() 升,这天下午小李共耗油多少升?
升,这天下午小李共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2﹣4ac>0;④a+b+c<0;⑤4a﹣2b+c<0,其中正确的个数是( ) 
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点).有下列结论: ①当x=3时,y=0;
②3a+b>0;
③﹣1≤a≤﹣ ![]() ;
;
④ ![]() ≤n≤4.
≤n≤4.
其中正确的有( )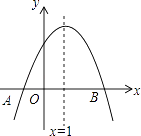
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com