Question

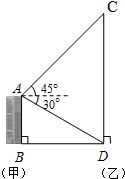
13．如图，甲楼AB的高度为50米，自甲楼楼顶A处，测得乙楼顶端C处的仰角为45°，测得乙楼底部D处的俯角为30°，求乙楼CD的高度（结果精确到1米，$\sqrt{3}$取1.73）．

Answer 1

分析 首先分析图形，根据题意构造直角三角形．本题涉及多个直角三角形，应利用其公共边构造关系式求解．

解答 解：过点A 作AE⊥CD，
在Rt△AED中，∵AB=DE=50，tan∠EAD=$\frac{DE}{AE}=\frac{{\sqrt{3}}}{3}$，
∴$AE=50\sqrt{3}$．
在Rt△AEC中，∵∠CAE=45°，
∴$CE=AE=50\sqrt{3}$，
∴$CD=CE+DE=50\sqrt{3}+50≈87$（米）．
∴CD=CE+DE=50（1+$\sqrt{3}$）=136.5≈137（米）

点评 此题考查了解直角三角形的应用-仰角俯角问题，本题要求学生借助俯角构造直角三角形，并结合图形利用三角函数解直角三角形．