
分析 根据题意,将圆按逆时针方向依次标记三点为A、B、C,设出弧AB、弧AC、弧BC的长度,得到所有可能结果构成的平面区域与“三点组成锐角三角形”构成的平面区域,分别计算出两个区域的面积,再利用几何概型公式加以计算,可得构成锐角或直角三角形的概率,即可得出结论.
解答 解:圆上任取三点所构成的三角形是钝角三角形是随机事件,
如图1,设圆的半径为1,按逆时针方向依次表记三点为A、B、C,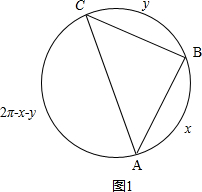
设弧AB=x,弧BC=y,弧AC=2π-x-y,
依题意,所有可能的结果构成的平面区域为:Ω={(x,y)|0<x<2π,0<y<2π,0<2π-x-y<2π},
事件A=“三点组成锐角或直角三角形”,构成的平面区域为:A={(x,y)∈Ω|0<x≤π,0<y<π,0<2π-x-y<π},
分别作出Ω与A中不等式组对应的平面区域,得到两个三角形及其内部区域,如图2所示,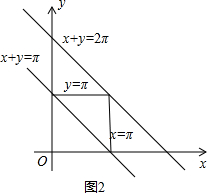
∵平面区域Ω的面积为2π2,平面区域A的面积为$\frac{1}{2}$×π×π=$\frac{1}{2}$π2,
∴所求概率为:P(A)=$\frac{1}{4}$,
∴圆上任取三点所构成的三角形是钝角三角形的概率为1-$\frac{1}{4}$=$\frac{3}{4}$.
点评 本题给出圆周上的任意三点,求此三点构成钝角三角形的概率,着重考察了圆内接三角形、二元一次不等式组表示的平面区域和几何概型计算公式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第_____块去,这利用了三角形全等中的_____原理( )
小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第_____块去,这利用了三角形全等中的_____原理( )| A. | 2;SAS | B. | 4;ASA | C. | 2;AAS | D. | 4;SAS |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1cm、2cm、3cm、4cm | B. | 3cm、5cm、9cm、15cm | ||
| C. | 2cm、4cm、6cm、8cm | D. | 1cm、3cm、5cm、7cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 探究题
探究题查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com