
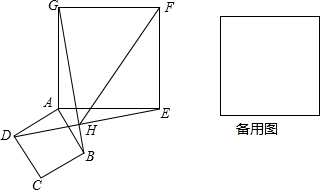
 如图,已知正方形ABCD、AEFG边长分别为$\sqrt{2}$cm、2cm,将正方形ABCD绕点A旋转,连接BG、DE相交于点H.
如图,已知正方形ABCD、AEFG边长分别为$\sqrt{2}$cm、2cm,将正方形ABCD绕点A旋转,连接BG、DE相交于点H.分析 (1)利用正方形的性质得出AD=AB,AE=AG,∠DAB=∠GAE=90°,进而得出∠DAE=∠BAG即可判断出△ADE≌△BAG,最后用互余即可判断出DE⊥BG;
(2)①判断出点H是正方形ABCD的外接圆上,即可得出结论;
②先判断出点H的运动轨迹,即可得出结论.
解答 解:DE=BG,DE⊥BG,
理由:如图,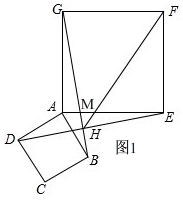
∵四边形ABCD和四边形AEFG是正方形,
∴AD=AB,AE=AG,∠DAB=∠EAG=90°,
∴∠DAE=∠BAG,
在△ADE和△ABG中,$\left\{\begin{array}{l}{AD=AB}\\{∠DAE=∠BAG}\\{AE=AG}\end{array}\right.$,
∴△ADE≌△ABG,
∴DE=BG,∠AED=∠AGB,
∵∠AGB+∠AMG=90°,
∴∠AED+∠AMG=90°,
∵∠AMG=∠EMH,
∴∠AED+∠EMH=90°,
∴∠EHG=90°,
∴DE⊥BG;
即:DE=BG,DE⊥BG;
(2)①由(1)知,∠EHG=90°=∠C,
∴点H是正方形ABCD的外接圆上,
∴DH是正方形ABCD的外接圆的弦,
∴DH最大就是正方形ABCD的外接圆的直径BD=2;
故答案为2;
②如图2,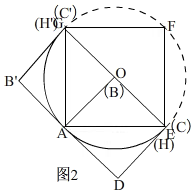 作出正方形AEFG的外接圆,
作出正方形AEFG的外接圆,
连接OC',OC,FC,FC',
由(1)知,∠EHG=90°=∠EFG,
∴点H在正方形AEFG的外接圆⊙O上,
点H的运动轨迹是如图2所示的$\widehat{CAC'}$这段弧,
∴当∠AGH越大,$\widehat{AC}$越长,
即:GH⊥AB时,∠AGH最大,
在Rt△ABG中,AB=$\sqrt{2}$,AG=2,
∴sin∠AGB=$\frac{AB}{AG}=\frac{\sqrt{2}}{2}$,
∴∠AGH=45°,
即:点H,C,E重合,
∴点H的运动轨迹是正方形AEFG的半圆,
∴点H经过路线的长度为$\frac{1}{2}$•2π•$\sqrt{2}$=$\sqrt{2}$π.
点评 此题是几何变换综合题,主要考查了正方形的性质,全等三角形的判定和性质,垂直的证明,判断点在圆上的方法,解(1)的关键是判断出△ADE≌△BAG,解(2)的关键是判断出点H在正方形ABCD和正方形AEFG的外接圆上,是一道中等难度的中考常考题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:填空题
 如图,平行四边形ABCD中,点E、F分别在AD、AB上,依次连接EB、EC、FC、FD,图中阴影部分的面积分别为S1、S2、S3、S4,已知S1=2、S2=12、S3=3,则S4的值是7.
如图,平行四边形ABCD中,点E、F分别在AD、AB上,依次连接EB、EC、FC、FD,图中阴影部分的面积分别为S1、S2、S3、S4,已知S1=2、S2=12、S3=3,则S4的值是7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
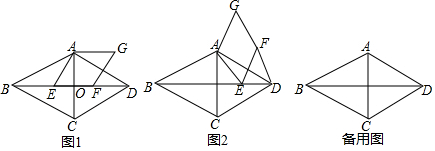
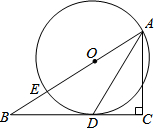 如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD.
如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
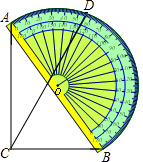 如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )
如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )| A. | 63° | B. | 54° | C. | 36° | D. | 27° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
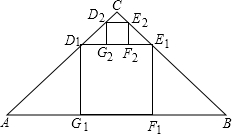 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,在Rt△ABC内部作正方形D1E1F1G1,其中点D1,E1分别在AC,BC边上,边F1G1在BC上,它的面积记作S1;按同样的方法在△CD1E1内部作正方形D2E2F2G2,它的面积记作S2,S2=$\frac{8}{{3}^{4}}$,…,照此规律作下去,正方形DnEnFnGn的面积Sn=$\frac{8}{{3}^{2n}}$.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,在Rt△ABC内部作正方形D1E1F1G1,其中点D1,E1分别在AC,BC边上,边F1G1在BC上,它的面积记作S1;按同样的方法在△CD1E1内部作正方形D2E2F2G2,它的面积记作S2,S2=$\frac{8}{{3}^{4}}$,…,照此规律作下去,正方形DnEnFnGn的面积Sn=$\frac{8}{{3}^{2n}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
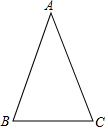 如图,在△ABC中,AB=AC.
如图,在△ABC中,AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com