已知扇形的圆心角为120°,面积为300πcm2.
(1)求扇形的弧长;
(2)若将此扇形卷成一个圆锥,则这个圆锥的轴截面面积为多少?
【答案】
分析:(1)根据扇形面积公式S=

求得半径R,再根据l=

求弧长;
(2)由1的弧长为底面周长求得底面半径,由勾股定理求得圆锥的高,再根据三角形的面积公式求得面积.
解答: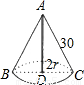
解:(1)∵300π=

,
∴R=30,
∴弧长L=20π(cm);
(2)如图所示:
∵20π=2πr,
∴r=10,R=30,
AD=
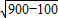
=20
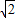
,
∴S
轴截面=

×BC×AD=

×2×10×20

=200

(cm
2).
答:扇形的弧长是20πcm卷成圆锥的轴截面是200
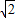
cm
2.
点评:本题利用了勾股定理,扇形的面积公式,弧长公式,圆周长公式求解.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案