
����Ŀ����ͼ1����֪�������µ�������y1=ax2��2ax+1����A��m��1������y�ύ�ڵ�C������ΪB����������y1�Ƶ�C��ת180���õ�������y2 �� ��A��B�Ķ�Ӧ��ֱ�Ϊ��D��E��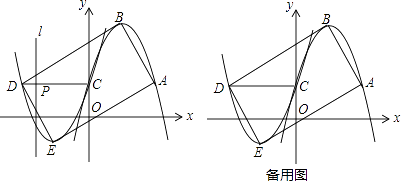
��1��ֱ��д����A��C��D�����ꣻ
��2�����ı���ABCD�Ǿ���ʱ����a��ֵ��������y2�Ľ���ʽ��
��3���ڣ�2���������£�����DC���߶�DC�ϵĶ���P�ӵ�D��������ÿ��1����λ���ȵ��ٶ��˶�����Cֹͣ���ڵ�P�˶��Ĺ����У�����P��ֱ��l��x�ᣬ������ABDE��ֱ��l�۵���������۵�����غϲ������ΪSƽ����λ����P���˶�ʱ��Ϊt�룬��S��t�ĺ�����ϵ��
���𰸡�
��1��
�⣺������ã�
��A��m��1������y1=ax2��2ax+1�ã�am2��2am+1=1��
��ã�m1=2��m2=0���ᣩ��
��A��2��1����C��0��1����D����2��1����
��2��
�⣺��ͼ1��
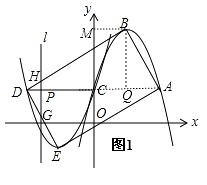
�ɣ�1��֪��B��1��1��a��������B��BM��y�ᣬ
���ı���ABDEΪ���Σ���BC=CD��
��BM2+CM2=BC2=CD2��
��12+����a��2=22��
��a= ![]()
![]() ��
��
��y1�����߿������£�
��a=�� ![]() ��
��
��y2��y1�Ƶ�C��ת180��õ�����E����1��1�� ![]() ����
����
����y2=a��x+1��2+1�� ![]() ����a=
����a= ![]() ��
��
��y2= ![]() x2+2
x2+2 ![]() x+1��
x+1��
��3��
�⣺��ͼ2��
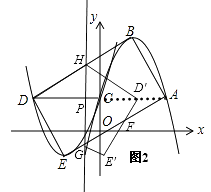
��0��t��1ʱ����DP=t������ֱ�ǡ�BQD��
��BQ= ![]() ��DQ=3����BD=2
��DQ=3����BD=2 ![]() ��
��
���BDQ=30�㣬
��PH= ![]() t��PG=
t��PG= ![]() t��
t��
��S= ![]() ��PE+PF����DP=
��PE+PF����DP= ![]() t2��
t2��
��ͼ2����1��t��2ʱ��EG=E��G= ![]() ��t��1����E��F=2��t��1����
��t��1����E��F=2��t��1����
S���غ�= ![]() ��t��1��2��
��t��1��2��
S=S1+S2��S���غ�= ![]() +
+ ![]() ��t��1����
��t��1���� ![]() ��t��1��2��
��t��1��2��
=�� ![]()
����������S= ![]() t2��0��t��1����S=��
t2��0��t��1����S=�� ![]() ��1��t��2����
��1��t��2����
�����������⿼���˶��κ��������ʣ���ת�����ʺ;��ζԽ��ߵ����ʣ��Լ����Ǻ���������ǵ�Ӧ�ã��ۺ��Խ�ǿ�����ڴ���֪���ھ����������DZ���Ĺؼ����������Լ�����εı߳����Խ�����ߵļнǣ��ó�30�㣬�Դ�Ϊͻ�ƿڣ�����Ҫ�ı߳���t��ʾ���ó�������ϵʽ�����Ȿ������˷������۵�˼�룬���ڶ��κ��������ý϶࣬Ӧ�������գ���1��ֱ�ӽ���A���������y1=ax2��2ax+1�ó�m��ֵ����Ϊ��ͼ���֪��A�ڵ�һ���ޣ�����m��0����m=2��д��A��C�����꣬��D���A���ڵ�C�Գƣ��ɴ�д����D�����ꣻ��2�����ݶ������깫ʽ�ó�������y1�Ķ���B�����꣬���ɾ��ζԽ��������ƽ�ֵã�BC=CD����ֱ�ǡ�BMC�У��ɹ��ɶ����з������a��ֵ�ó�������y1�Ľ���ʽ������ת�����ʵó�������y2�Ľ���ʽ����3��������������ۣ��ٵ�0��t��1ʱ��S=S��GHD=S��PDH+S��PDG �� �������߹���ֱ�������Σ����PG��PH�����������ʽ���㣻�ڵ�1��t��2ʱ��S=Sֱ��������+S������S���غ� �� ���ﲻ�غϵ�ͼ�ξ��ǡ�GE��F������30��Ǻ�60��ǵ�ֱ�������ε����ʽ��м���ó����ۣ�
�����㾫����ͨ��������ö��κ��������ʺ;��ε����ʣ����������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С�����ε��ĸ��Ƕ���ֱ�ǣ����εĶԽ�����ȼ����Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��MN��EF�����滥��ƽ�еľ��棬һ������AB���䵽����MN�ϣ��������ΪBC������1=��2��
��1���ó߹���ͼ��������BC������EF�����ķ������CD��
��2�����ж�AB��CD��λ�ù�ϵ��
��3���������˼���ģ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y=�� ![]() x+3��������ֱ��ڵ�A��B����P��������y=��
x+3��������ֱ��ڵ�A��B����P��������y=�� ![]() ��x��
��x�� ![]() ��2+4�ϣ���ʹ��ABPΪ���������εĵ�P�ĸ����У�������
��2+4�ϣ���ʹ��ABPΪ���������εĵ�P�ĸ����У�������
A.3��
B.4��
C.5��
D.6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ֳ��ĸ�С�����Σ�Ȼ��ͼ�ڵķ�ʽƴ��һ��������.
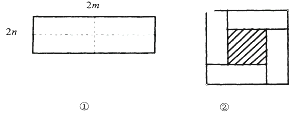
(1)����Ϊͼ���е���Ӱ���ֵ������εı߳�����_________________.
(2)�������ֲ�ͬ�ķ����д���ʽ��ʾͼ������Ӱ���ֵ����.
������_________________________________________________________.
������_________________________________________________________.
(3)�۲�ͼ�ڣ�����д��(m+n)2��(m-n)2��mn����������ʽ��ĵ�����ϵ��?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��AB��DF����D+��B=180����

��1����֤��DE��BC��
��2�������AMD=75�������AGC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����г��ӽ���ѵ����ѵ��ʱ���ж�Ա������ͬ���ٶ�ǰ����ͻȻ��1�Ŷ�Ա��ÿСʱ��������Ա��10ǧ���ٶȶ����н����н���10ǧ���ת��ͷ���ٶȲ��������ֱ���������Ķ�Ա��ϣ���1�Ŷ�Ա��ӿ�ʼ����������Ա���»�ϣ�������15���ӣ�
��1��������Ա���н��ٶ��Ƕ��٣�
��2��1�Ŷ�Ա����ӿ�ʼ�����Ա���»����������У������ʱ����������Ա���1ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���жԽ�����Ϊ10Ԫ/ǧ�˵�ij��ƻ���������������ͳ�ƣ�����ÿ��������y��ǧ�ˣ������ۼ�x��Ԫ/ǧ�ˣ�����һ�κ�����ϵ����ͼ��ʾ�� 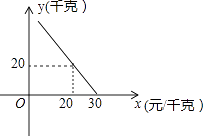
��1����y����x�ĺ�����ϵʽ����Ҫ��д��x��ȡֵ��Χ����
��2��Ӧ����ȷ�����ۼۣ�ʹ��Ʒ��ƻ����ÿ���������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�CA=CB����ACB=90�㣬AB=2����DΪAB���е㣬�Ե�DΪԲ����Բ�Ľ�Ϊ90�������DEF����Cǡ�ڻ�EF�ϣ���ͼ����Ӱ���ֵ����Ϊ��������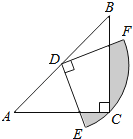
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
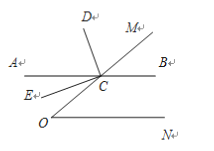
����Ŀ����֪����ͼ����C�ڡ�MON��һ��OM�ϣ�����C��ֱ��AB��ON��CDƽ�֡�ACM��CE��CD��
��1������O=50�㣬���BCD�Ķ�����
��2����֤��CEƽ�֡�OCA��
��3������OΪ���ٶ�ʱ��CA�֡�OCD��1��2�����֣���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com