
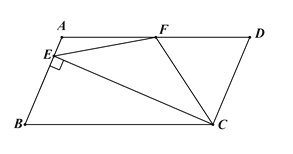
【题目】如图,在平行四边形 ABCD 中, AD 2 AB ;CF 平分 BCD 交 AD 于 F ,作 CE AB , 垂足 E 在边 AB 上,连接 EF .则下列结论:① F 是 AD 的中点; ② S△EBC 2S△CEF;③ EF CF ; ④ DFE 3AEF .其中一定成立的是_____.(把所有正确结论的序号都填在横线上)
【答案】①③④.
【解析】
由角平分线的定义和平行四边形的性质可证得CD=DF,进一步可证得F为AD的中点,由此可判断①;延长EF,交CD延长线于M,分别利用平行四边形的性质以及①的结论可得△AEF≌△DMF,结合直角三角形的性质可判断③;结合EF=FM,利用三角形的面积公式可判断②;在△DCF和△ECF中利用等腰三角形的性质、外角的性质及三角形内角和可得出∠DFE=3∠AEF,可判断④,综上可得答案.
解:∵四边形ABCD为平行四边形,∴AD∥BC,
∴∠DFC=∠BCF,
∵CF平分∠BCD,∴∠BCF=∠DCF,
∴∠DFC=∠DCF,∴CD=DF,
∵AD=2AB,∴AD=2CD,
∴AF=FD=CD,即F为AD的中点,故①正确;
延长EF,交CD延长线于M,如图,
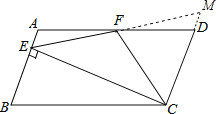
∵四边形ABCD是平行四边形,∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,∴AF=FD,
又∵∠AFE=∠DFM,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,∴∠AEC=90°,
∴∠ECD=∠AEC=90°,
∵FM=EF,∴FC=FM,故③正确;
∵FM=EF,∴![]() ,
,
∵MC>BE,
∴![]() <2
<2![]() ,故②不正确;
,故②不正确;
设∠FEC=x,则∠FCE=x,
∴∠DCF=∠DFC=90°-x,
∴∠EFC=180°-2x,
∴∠EFD=90°-x+180°-2x=270°-3x ,
∵∠AEF=90°-x,
∴∠DFE=3∠AEF,故④正确;
综上可知正确的结论为①③④.
故答案为①③④.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】如图①,若二次函数![]() 的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数
的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数![]() 的图象的对称点为C。
的图象的对称点为C。
(1)求b、c的值;
(2)证明:点C 在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数![]() 的图象于点D,连结AC,交正比例函数
的图象于点D,连结AC,交正比例函数![]() 的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图所示的规律摆放:第1上图形有6个小圆,第2个图形有10个小圆,和3个图形有16个小圆,第4个图形有24个小圆,…依此规律,第7个图形的小圆的个数是_____,第n个图形的小圆的个数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电业局要对某市区的电线路进行巡检,某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,检修车一天中八次行驶记录如下:(单位:km)-4,+7,-9,+8,+6,-5,-2,-4
(1)求收工时检修小组在A地的什么方向?距A地多远?
(2)若每千米耗油0.5升,当维修小组返回到A地时,问共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体, 甲、乙容器的内底面半径分别为![]() 和
和![]() ,现将一个半径为
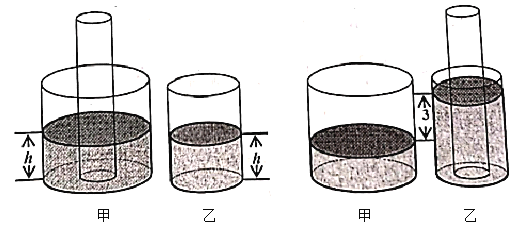
,现将一个半径为![]() 的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为
的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为![]() (如图甲),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高
(如图甲),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高![]() (如图乙).
(如图乙).
(1)求甲、乙两个容器的内底面面积.
(2)求甲容器内液体的体积(用含![]() 的代数式表示).
的代数式表示).
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B在数轴上分别表示有理数a,b.A,B两点之间的距离表示为AB,在数轴上A,B两点之间的距离AB=|a﹣b|.利用数形结合思想回答下列问题:
(1)数轴上表示﹣2和8两点之间的距离是________.
(2)数轴上表示x和﹣4两点A和B之间的距离表示为__________;如果AB=2,那么x=___________.
(3)若点C表示的数为x,当点C在什么位置时,|![]() x+1|+|
x+1|+|![]() x1|取得的值最小,并直接写出最小值。
x1|取得的值最小,并直接写出最小值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为a,点B表示的数为b,且满足![]() .
.
(1)写出a、b及AB的距离:a=________;b=________;AB=________.
(2)若动点P从点A出发,以每秒3个点位长度沿数轴向右匀速运动,动点Q从点B出发,以每秒5个单位长度向右匀速运动,若P、Q同时出发,问点Q运动多少秒追上点P?
![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com