
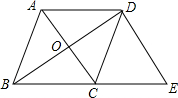
 如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE∥AC交BC的延长线于E.
如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE∥AC交BC的延长线于E.分析 (1)只要证明OC是△BDE的中位线即可.
(2)在RT△AOB中求出OA,再求出DE、BE即可解决问题.
解答  (1)证明:∵四边形ABCD是菱形,
(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,
∵DE∥OC,
∴BC=BE,
∴OC=$\frac{1}{2}$DE.
(2)解:在RT△AOB中,∵AB=5,OB=$\frac{1}{2}$BD=4,
∴AO=OC=$\sqrt{A{B}^{2}-O{B}^{2}}$=3,
∴DE=2OC=6,
∵BE=2BC=2AB=10,
∴△DBE周长=8+6+10=24.
点评 本题考查菱形的性质、三角形中位线定理、三角形周长等知识,解题的关键是证明点C是BE中点,记住菱形的对角线互相垂直,属于中考常考题型.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这80名学生是总体的一个样本 | B. | 80名学生是样本容量 | ||
| C. | 每名学生的体重是个体 | D. | 720名学生是总体 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一批炮弹的杀伤半径 | |
| B. | 了解扬州电视台《关注》栏目的收视率 | |
| C. | 了解长江中鱼的种类 | |
| D. | 了解某班学生最喜爱的体育项目 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com