
【题目】关于x的二次函数![]() (k为常数)和一次函数
(k为常数)和一次函数![]() .
.
(1)求证:函数![]() 的图象与x轴有交点.
的图象与x轴有交点.
(2)已知函数![]() 的图象与x轴的两个交点间的距离等于3,
的图象与x轴的两个交点间的距离等于3,
①试求此时k的值.
②若![]() ,试求x的取值范围.
,试求x的取值范围.
【答案】(1)见解析;(2)①k1=1,k2=![]() ;②当k=1时x<– 2或 x>2,当k=
;②当k=1时x<– 2或 x>2,当k=![]() 时,10<x<– 2.
时,10<x<– 2.
【解析】
(1)证明△=b2-4ac≥0,便可得结论;
(2)①函数y1的图象与x轴的两个交点间的距离等于3,根据根与系数的关系列出k的方程,便可求解;
②分k=1和k=![]() 两种情况,依据y1>y2列出关于x的不等式,解之可得.
两种情况,依据y1>y2列出关于x的不等式,解之可得.
解:(1)证明:△=(2k1)2+8 k=4k24k+1+8k=(2k+1)2≥0,
∴函数y1=kx2+(2k1) x 2的图象与x轴有交点.
(2)解:①设![]() 的两根为
的两根为![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() 函数
函数![]() 的图象与
的图象与![]() 轴的两个交点间的距离等于3,
轴的两个交点间的距离等于3,
![]() ,
,
![]()
![]() ,
,
解得,![]() 或
或![]() ;
;
②I.当k=1时,y1= x2+ x – 2,画出y1= x2+ x – 2和y2=x+2的图象,如图1所示,
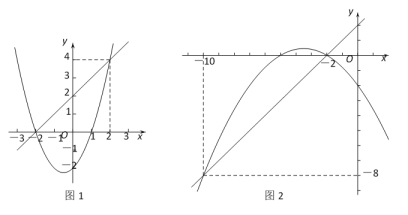
由图知,y1与y2的交点分别为(2,0)和 (2,4),
∴当y1>y2时x<– 2或 x>2;
II.当k=![]() 时,y1=
时,y1=![]() x2
x2![]() x – 2,
x – 2,
画出y1=![]() x2
x2![]() x – 2和y2=x+2的图象,如图2所示,
x – 2和y2=x+2的图象,如图2所示,
由图知,y1与y2的交点分别为(2,0)和 (10,8),
∴当y1>y2时10<x<– 2.
综上所述,当k=1时x<– 2或 x>2,当k=![]() 时,10<x<– 2.
时,10<x<– 2.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
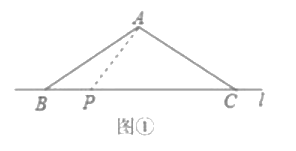
【题目】数学兴趣活动课上,小致将等腰![]() 的底边
的底边![]() 与直线
与直线![]() 重合.
重合.
(1)如图![]() ,在
,在![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 所在的直线
所在的直线![]() 上移动,根据“直线外一点到直线上所有点的连线中垂线段最短”,小致发现
上移动,根据“直线外一点到直线上所有点的连线中垂线段最短”,小致发现![]() 的最小值是____________.
的最小值是____________.
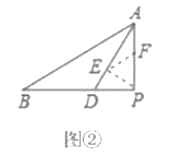
(2)为进一步运用该结论,在(1)的条件下,小致发现,当![]() 最短时,如图
最短时,如图![]() ,在
,在![]() 中,作
中,作![]() 平分
平分![]() 交
交![]() 于点
于点![]() 点
点![]() 分别是边
分别是边![]() 上的动点,连结
上的动点,连结![]() 小致尝试探索
小致尝试探索![]() 的最小值,小致在
的最小值,小致在![]() 上截取
上截取![]() 使得
使得![]() 连结
连结![]() 易证
易证![]() ,从而将
,从而将![]() 转化为
转化为![]() 转化到(1)的情况,则
转化到(1)的情况,则![]() 的最小值为 ;
的最小值为 ;
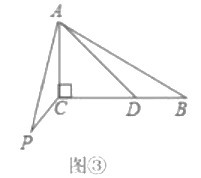
(3)解决问题:如图![]() ,在
,在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上的动点,连结
上的动点,连结![]() 将线段
将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() 连结
连结![]() ,求线段
,求线段![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,过点P(0,a)作直线l分别交![]()
![]() 于点M、N,
于点M、N,
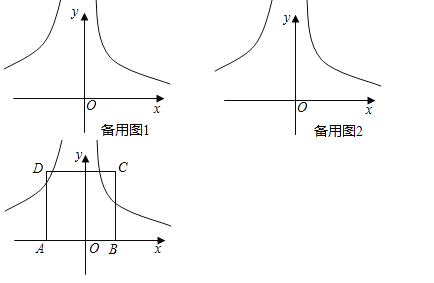
(1)若m=4,MN∥x轴,![]() ,求n的值;
,求n的值;
(2)若a=5,PM=PN,点M的横坐标为3,求m-n的值;
(3)如图,若m=4,n=-6,点A(d,0)为x轴的负半轴上一点,B为x轴上点A右侧一点,AB=4,以AB为一边向上作正方形ABCD,若正方形ABCD与![]()
![]() 都有交点,求d的范围.
都有交点,求d的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将直角三角形纸片![]() (
(![]() ,
,![]() )沿过点A的直线折叠,使得AC落在AB边上折痕为AD,展开纸片(如图1);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到
)沿过点A的直线折叠,使得AC落在AB边上折痕为AD,展开纸片(如图1);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到![]() (如图2),若
(如图2),若![]() ,
,![]() ,则折痕EF的长为( )
,则折痕EF的长为( )
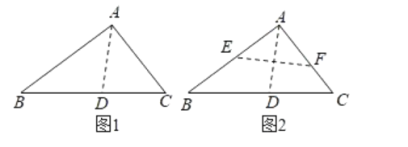
A.![]() B.
B.![]() C.
C.![]() D.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
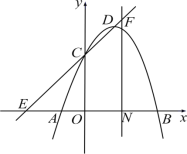
【题目】已知抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为D,直线CD与x轴交于点E.
(1)求A、B的坐标;
(2)求点E的坐标;
(3)过线段OB的中点N作x轴的垂线并交直线CD于点F,则直线NF上是否存在点M,使得点M到直线CD的距离等于点M到原点O的距离?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冬季来临,某网店准备在厂家购进![]() ,
,![]() 两种暖手宝共
两种暖手宝共![]() 个用于销售,若购买
个用于销售,若购买![]() 种暖手宝
种暖手宝![]() 个,
个,![]() 种暖手宝
种暖手宝![]() 个,需要
个,需要![]() 元;若购买
元;若购买![]() 种暖手宝
种暖手宝![]() 个,
个,![]() 种暖手宝
种暖手宝![]() 个,则需要
个,则需要![]() 元
元
(1)购买![]() ,
,![]() 两种暖手宝每个各需多少元?
两种暖手宝每个各需多少元?
(2)①由于资金限制,用于购买这两种暖手宝的资金不能超过![]() 元,设购买
元,设购买![]() 种暖手宝
种暖手宝![]() 个,求
个,求![]() 的取值范围;
的取值范围;
②在①的条件下,购进![]() 种暖手宝不能少于
种暖手宝不能少于![]() 个,则有哪几种购买方案?
个,则有哪几种购买方案?
(3)购买后,若一个![]() 种暖手宝运费为
种暖手宝运费为![]() 元,一个
元,一个![]() 种暖手宝运费为
种暖手宝运费为![]() 元,在第
元,在第![]() 问的各种购买方案中,购买
问的各种购买方案中,购买![]() 个暖手宝,哪一种购买方案所付的运费最少?最少运费是多少元?
个暖手宝,哪一种购买方案所付的运费最少?最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
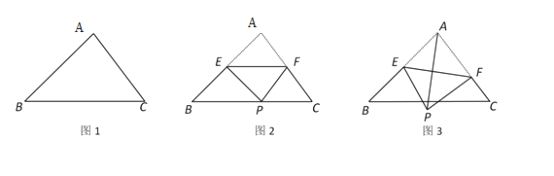
【题目】如图,在△ABC中,AB=![]() ,∠B=45°,∠C=60°.
,∠B=45°,∠C=60°.
(1)求BC边上的高线长.
(2)点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.
①如图2,当点P落在BC上时,求∠AEP的度数.
②如图3,连结AP,当PF⊥AC时,求AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com