
分析 (1)先利用坐标轴上点的特点确定出点A,B坐标,进而得出BC=b-a,再利用点A,D坐标的得出AD=b-a=BC,另为利用A,D点的坐标特点得出AD∥BC即可得出结论;
(2)①利用对称性和(1)中得出的四边形ABCD是平行四边形,即可得出S△BC'D'=S△BCD,根据三角形的面积公式得出S△BC'D'=a(3-a),建立方程,判断出此方程无解,即可得出不存在满足条件的a,使得△BC′D′面积为$\frac{5}{2}$;
②利用同角的余角相等得出,∠CC'O=∠ABO进而得出∠△CC'O∽△ABO,得出C'O=$\frac{b}{2}$,最后用勾股定理即可得出结论.
解答 解:(1)四边形ABCD是平行四边形,
理由:
∵直线y=-$\frac{1}{2}$x+a(a>0)?分别与x 轴、y 轴交于A、B 两点,
∴A(2a,0),B(0,a),
∵C(0,b)、(b>a).
∴BC=b-a,
∵D(2a,b-a).
∴AD=b-a=BC,
∵A(2a,0),D(2a,b-a).
∴AD∥BC,
∴四边形ABCD是平行四边形,
(2)①不存在满足条件的a,使得△BC'D'的面积为$\frac{5}{2}$,
理由:如图1,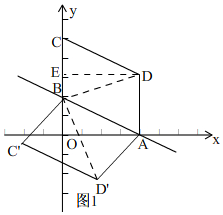 连接BD,BD',过点D作DE⊥y轴于E,
连接BD,BD',过点D作DE⊥y轴于E,
∴DE=OA=2a,
∵点C、D关于直线AB的对称点分别为C′、D′.
∴S平行四边形ABC'D'=S平行四边形ABCD,
∵DB,BD'分别是平行四边形ABCD,ABC'D的对角线,
∴S△BC'D'=S△BCD=$\frac{1}{2}$BC•DE=$\frac{1}{2}$(b-a)•2a=a(b-a),
∵b=3,
∴S△BC'D'=a(3-a),
假设存在存在满足条件的a,使得△BC′D′面积为$\frac{5}{2}$,
∴a(3-a)=$\frac{5}{2}$,
∴2a2-6a+5=0,
而△=36-4×2×5=-4<0,
∴此方程无解,
假设错误,
∴不存在满足条件的a,使得△BC'D'的面积为$\frac{5}{2}$,
②如图2,
连接CC',则直线AB垂直平分线CC',
∴∠CC'O+∠C'AB=90°,
∵∠C'AB+∠ABO=90°,
∴∠CC'O=∠ABO,
∵∠COC'=∠AOB=90°,
∴△CC'O∽△ABO,
∴$\frac{CO}{AO}=\frac{C'O}{BO}$,
∴$\frac{b}{2a}=\frac{C'O}{a}$,
∴C'O=$\frac{b}{2}$,
由轴对称的性质得,BC'=BC=b-a,
在Rt△BC'O中,OB2+C'O2=C'B2,
∴a2+($\frac{b}{2}$)2=(b-a)2,
∴3b2-8ab=b(3b-8a)=0,
∵b>a>0,
∴3b-8a=0,
∴$\frac{a}{b}=\frac{3}{8}$,
∴a 与b的函数表达式a=$\frac{3}{8}$b(b>0).
点评 此题是一次函数综合题,主要考查了平行四边形的判定和性质,相似三角形的性质和判定,三角形的面积公式,勾股定理轴对称的性质,一元二次方程的根的判别式等知识点,体现了数形结合的思想,判定出四边形ABCD是平行四边形是解本题的关键.


科目:初中数学 来源: 题型:选择题
| 甲 | 乙 | 丙 | |
| $\overline{x}$ | 8 | 9 | |
| s2 | 1 | 1.2 |
| A. | $\overline x=8$,S2=0.7 | B. | $\overline x=8$,S2=1.2 | C. | $\overline x=9$,S2=1 | D. | $\overline x=9$,S2=1.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
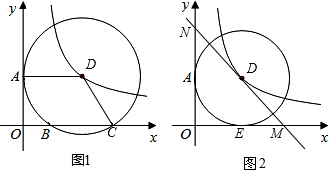
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
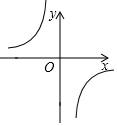 已知函数y=$\frac{m}{x}$的图形如图,以下结论:
已知函数y=$\frac{m}{x}$的图形如图,以下结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
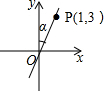 如图,在平面直角坐标系中,直线OP过点(1,3),则tanα的值是( )
如图,在平面直角坐标系中,直线OP过点(1,3),则tanα的值是( )| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com