
分析 (1)根据多项式乘以多项式进行计算即可;
(2)根据平方差公式和完全平方公式进行计算即可;
(3)根据零指数幂、负整数指数幂进行计算即可;
(4)根据多项式除以单项式进行计算即可.
解答 解:(1)原式=x2-4-x2+2x+3
=2x-1;
(2)原式=[(3x+1)-2y][(3x+1)+2y]
=(3x+1)2-4y2
=9x2+6x+1-4y2;
(3)原式=1+4-1
=4;
(4)原式=45a2÷(-$\frac{1}{3}$a)-$\frac{1}{6}$a2b÷(-$\frac{1}{3}$a)+3a÷(-$\frac{1}{3}$a)
=-135a+$\frac{1}{2}$ab-9.
点评 本题考查了整式的混合运算,掌握多项式乘以多项式的法则、零指数幂、负整数指数幂以及平方差公式和完全平方公式是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
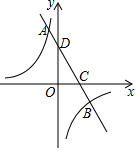 已知直线y=mx+4与反比例函数y=$\frac{k}{x}$(k<0)的图象交于A,B两点,与x轴,y轴分别交于点C,D,OD=2OC,点A的纵坐标为6.
已知直线y=mx+4与反比例函数y=$\frac{k}{x}$(k<0)的图象交于A,B两点,与x轴,y轴分别交于点C,D,OD=2OC,点A的纵坐标为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
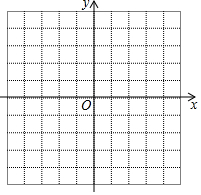 如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,建立如图所示的平面直角坐标系,已知点A(1,0),B(4,0),C(3,3),D(1,4)
如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,建立如图所示的平面直角坐标系,已知点A(1,0),B(4,0),C(3,3),D(1,4)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
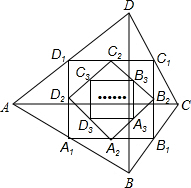 如图,四边形ABCD中,对角线AC⊥BD,且AC=2,BD=2,各边中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再各取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,以此类推,这样得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为21-n.
如图,四边形ABCD中,对角线AC⊥BD,且AC=2,BD=2,各边中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再各取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,以此类推,这样得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为21-n.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
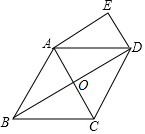 已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com