
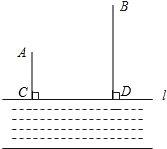
 如图,A,B两个小镇在河流CD的同侧,到河的距离分别为AC=6千米,BD=14千米,且CD=15千米,现要在河边建一自来水厂,同时向A,B两镇供水,铺设水管的费用为每千米3万元,请你在河流CD上选择水厂的位置M,使铺设水管的费用最省,并求出总费用是多少?
如图,A,B两个小镇在河流CD的同侧,到河的距离分别为AC=6千米,BD=14千米,且CD=15千米,现要在河边建一自来水厂,同时向A,B两镇供水,铺设水管的费用为每千米3万元,请你在河流CD上选择水厂的位置M,使铺设水管的费用最省,并求出总费用是多少? 分析 根据题意,要使铺设水管的费用最省,则自来水厂与A、B两个小镇的距离和最小,所以作出点A关于直线l的对称点A′,连接BA′,则BA′与直线l的交点即是水厂的位置M,根据勾股定理,求出A′B的长度,再根据总价=单价×数量,即可得出答案.
解答 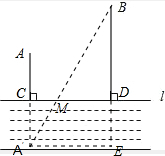 解:作点A关于直线CD的对称点A'.连接BA',交CD于点M,则A'B=AM+BM,
解:作点A关于直线CD的对称点A'.连接BA',交CD于点M,则A'B=AM+BM,
此时AM+BM为铺设水管的最短路线,
过A'作CD的平行线,交BD的延长线于点E,得Rt△A'BE,
∵DE=A'C=AC=6千米,BE=DE+BD=20千米,A'E=CD=15千米,∴A'B=$\sqrt{{{A}^{′}E}^{2}+E{B}^{2}}$=$\sqrt{1{5}^{2}+2{0}^{2}}$=25,
∴总费用是:3×25=75(万元).
点评 此题主要考查了轴对称-最短路线问题,用到的知识点是:直角三角形的性质、勾股定理的应用、总价=单价×数量,解答此题的关键是要明确:凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合所学轴对称变换来解决,多数情况要作点关于某直线的对称点.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{b}$=$\frac{{a}^{2}}{{b}^{2}}$ | B. | $\frac{a}{b}$=$\frac{a+c}{b+c}$ | C. | $\frac{a}{b}$=$\frac{a-c}{b-c}$ | D. | $\frac{a}{b}$=$\frac{ma}{mb}$(m≠0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com