
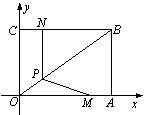
如图,将OA = 6,AB = 4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.
(1)点B的坐标为 ;用含t的式子表示点P的坐标为 ;(3分)
(2)记△OMP的面积为S,求S与t的函数关系式(0 < t < 6);并求t为何值时,S有最大值?(4分)
(3)试探究:当S有最大值时,在y轴上是否存在点T,使直线MT把△ONC分割![]() 成三角形和四边形两部分,且三角形的面积是△ONC面积的
成三角形和四边形两部分,且三角形的面积是△ONC面积的![]() ?若存在,求出点T的坐标;若不存在,
?若存在,求出点T的坐标;若不存在,![]() 请说明理由.(3分)
请说明理由.(3分)
 |  | ||
解:(1)解法一: 解法二:
∵AB为⊙O的直径, ∵AB为⊙O的直径,∠B=30°,
∴∠ACB=90°.……1分 ∴AC=![]() AB=1,BC=AB•cos30°=
AB=1,BC=AB•cos30°=![]()
∵在Rt△ABC中,∠B=30°,AB=2, ∵弦CD⊥直径AB于点M,
∴BC=AB•cos30°=2×![]() . ∴CD=2CM,AB×CM=AC×BC
. ∴CD=2CM,AB×CM=AC×BC
∵弦CD⊥直径AB,∠B=30°, ∴CD=2CM=2×![]()
∴ CM=![]() BC=
BC=![]() . =2×
. =2×![]() =
=![]()
CD=2CM=![]() . (其它解法请酌情给分)
. (其它解法请酌情给分)
(2)证明:∵AE切⊙O于点A,AB为⊙O的直径,
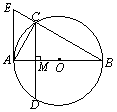 ∴∠BAE=90°,∠ACE=∠ACB=90°,
∴∠BAE=90°,∠ACE=∠ACB=90°,
∴∠ACE=∠BAE=90°.
又∵∠E=∠E,
∴Rt△ECA∽Rt△EAB.
∴![]() .
.
∴AE2=EB•EC. 26.解:(1)(6,4);(![]() ).(其中写对B点得1分)
).(其中写对B点得1分)
(2)∵S△OMP =![]() ×OM×
×OM×![]() ,
,
∴S =![]() ×(6 -t)×
×(6 -t)×![]() =
=![]() +2t.
+2t.
=![]() (0 < t <6).
(0 < t <6).
∴当![]() 时,S有最大值.
时,S有最大值.
(3)存在.
由(2)得:当S有最大值时,点M、N的坐标分别为:M(3,0),N(3,4),
则直线ON的函数关系式为:![]() .
.
设点T的坐标为(0,b),则直线MT的函数关系式为:![]() ,
,
 |
解方程组 得
得
∴直线ON与MT的交点R的坐标为![]() .
.
∵S△OCN =![]() ×4×3=6,∴S△ORT =
×4×3=6,∴S△ORT =![]() S△OCN =2.
S△OCN =2.
① 当点T在点O、C之间时,分割出的三角形是△OR1T1,如图,作R1D1⊥y轴,D1为垂足,则S△OR1T1=![]() ••••RD1•OT =
••••RD1•OT =![]() •
•![]() •b=2.
•b=2.
∴![]() , b =
, b =![]() .
.
∴b1 =![]() ,b2 =
,b2 =![]() (不合题意,舍去)
(不合题意,舍去)
此时点T1的坐标为(0,![]() ).
).
② 当点T在OC的延长线上时,分割出的三角形是△R2NE,如图,设MT交CN于点E,由①得点E的横坐标为![]() ,作R2D2⊥CN交CN于点D2,则
,作R2D2⊥CN交CN于点D2,则
S△R2NE=![]() •EN•R2D2 =
•EN•R2D2 =![]() •
•![]() •
•![]()
![]() =2.
=2.
∴![]() ,b=
,b=![]() .
.
∴b1=![]() ,b2=
,b2=![]() (不合题意,舍去).
(不合题意,舍去).
∴此时点T2的坐标为(0,![]() ).
).
综上所述,在y轴上存在点T1(0,![]() ),T2(0,
),T2(0,![]() )符合条件.
)符合条件.


科目:初中数学 来源: 题型:
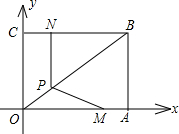 如图,将OA=6,AB=4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.
如图,将OA=6,AB=4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 4 |
| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题满分10分)
如图,将OA = 6,AB = 4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.
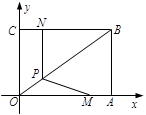
(1)点B的坐标为 ;用含t的式子表示点P的坐标为 ;(3分)
(2)记△OMP的面积为S,求S与t的函数关系式(0 < t < 6);并求t为何值时,S有最大值?(4分)
(3)试探究:当S有最大值时,在y轴上是否存在点T,使直线MT把△ONC分割成三角形和四边形两部分,且三角形的面积是△ONC面积的?若存在,求出点T的坐标;若不存在,请说明理由.(3分)
查看答案和解析>>
科目:初中数学 来源: 题型:
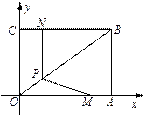
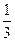 ?若存在,求出点T的坐标;若不存在,请说明理由.(3分)
?若存在,求出点T的坐标;若不存在,请说明理由.(3分)查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(湖北黄冈) 题型:解答题
(本题满分10分)
如图,将OA = 6,AB = 4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.
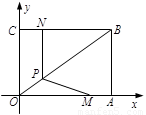
(1)点B的坐标为 ;用含t的式子表示点P的坐标为 ;(3分)
(2)记△OMP的面积为S,求S与t的函数关系式(0 < t < 6);并求t为何值时,S有最大值?(4分)
(3)试探究:当S有最大值时,在y轴上是否存在点T,使直线MT把△ONC分割成三角形和四边形两部分,且三角形的面积是△ONC面积的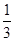 ?若存在,求出点T的坐标;若不存在,请说明理由.(3分)
?若存在,求出点T的坐标;若不存在,请说明理由.(3分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com