
【题目】已知方程组 ![]() .
.
(1)用含z的代数式表示x;
(2)若x,y,z都不大于10,求方程组的正整数解;
(3)若x=2y,z<m(m>0),且y>﹣1,求m的值.
【答案】
(1)解: ![]()
②﹣①×5,得
﹣4x+5z=﹣5,
解得,x= ![]() ,
,
(2)解:由题意可得,
x= ![]() ,且x≤10,y≤10,z≤10,
,且x≤10,y≤10,z≤10,
∴x= ![]() ≤10,得z≤7,
≤10,得z≤7,
∵x、y、z都是正整数,
∴当z=1时,x= ![]() 不符题意,
不符题意,
当z=2时,x= ![]() 不符题意,
不符题意,
当z=3时,x=5,则y=15﹣3﹣5=7,
当z=4时,x= ![]() 不符题意,
不符题意,
当z=5时,x= ![]() 不符题意,
不符题意,
当z=6时,x= ![]() 不符题意,
不符题意,
当z=7时,x=10,y=﹣2不符题意,
故方程组的正整数解是 ![]()
(3)解:∵x=2y,x= ![]() ,x+y+z=15,
,x+y+z=15,
解得,z= ![]() ,
,
∵z<m(m>0),
∴m的值是m> ![]()
【解析】(1)根据方程组可以用含z的代数式表示x,本题得以解决;(2)根据x与z的关系和x,y,z都不大于10,从而可以求得方程组的正整数解;(3)根据x=2y和x和z的关系以及方程组,可以得到z的值,从而可以得到m的值.
【考点精析】认真审题,首先需要了解解三元一次方程组(通过“代入”或“加减”消元,把“三元”化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而转化为解一元一次方程).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
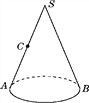
【题目】已知:如图,观察图形回答下面的问题:
(1)此图形的名称为________.
(2)请你与同伴一起做一个这样的物体,并把它沿AS剪开,铺在桌面上,则它的侧面展开图是一个________.
(3)如果点C是SA的中点,在A处有一只蜗牛,在C处恰好有蜗牛想吃的食品,但它又不能直接沿AC爬到C处,只能沿此立体图形的表面爬行,你能在侧面展开图中画出蜗牛爬行的最短路线吗?
(4)SA的长为10,侧面展开图的圆心角为90°,请你求出蜗牛爬行的最短路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一足球邀请赛,勇士队在第一轮比赛中共赛了9场,得分17分.比赛规定胜一场得3分,平一场得1分,负一场得0分.勇士队在这一轮中只负了2场,那么这个队胜了几场?又平了几场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今夏,十堰市王家河村瓜果喜获丰收,果农王二胖收获西瓜20吨,香瓜12吨,现计划租用甲、乙两种货车共8辆将这批瓜果全部运往外地销售,已知一辆甲种货车可装西瓜4吨和香瓜1吨,一辆乙种货车可装西瓜和香瓜各2吨.
(1)果农王二胖如何安排甲、乙两种货车可一次性地运到销售地?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王二胖应选择哪种方案,使运输费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
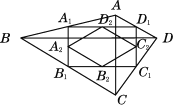
【题目】如图,在四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,…,如此进行下去,得到四边形AnBnCnDn.下列结论正确的是( )
①四边形A4B4C4D4是菱形;②四边形A3B3C3D3是矩形;③四边形A7B7C7D7的周长为![]() ;④四边形AnBnCnDn的面积为
;④四边形AnBnCnDn的面积为![]() .
.
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒.过点D作DF⊥BC于点F,连接DE,EF.当四边形AEFD是菱形时,t的值为( )

A. 20秒 B. 18秒 C. 12 秒 D. 6秒
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com