
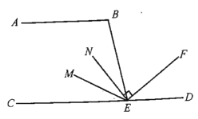
【题目】如图所示,![]() ,点E在CD上,EM和EN三等分
,点E在CD上,EM和EN三等分![]() ,
,![]() .①若
.①若![]() ,则
,则![]() __________;②当
__________;②当![]() __________时,
__________时,![]() .
.
【答案】![]()
![]()
【解析】
①首先根据平行线的性质可得∠CEB=75°,然后根据EM,EN三等分∠BEC可得∠NEB=25°,进而得到∠BEF的度数,然后再根据平角为180度计算出∠DEF的度数;
②当∠B=90°时,∠DEF=∠CEM;首先根据三等分线的性质可得∠CEM=∠MEN=∠BEN=30°,从而可得∠DEF=30°,进而得到∠DEF=∠CEM.
解:①∵∠B=105°,AB∥CD,
∴∠CEB=75°,
∵EM,EN三NE等分∠BEC,
∴∠CEM=∠MEN=∠BEN=25°,
∵EF⊥EN,
∴∠BEF=90°-25°=65°,
则∠DEF=180°-65°-75°=40°;
故答案为:40°;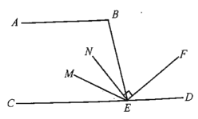
②当∠B=90°时,∠DEF=∠CEM;
∵AB∥CD,
∴∠B+∠CEB=180°,
∵∠B=90°,
∴∠CEB=∠BED=90°,
∵EM,EN三等分∠BEC,
∴∠CEM=∠MEN=∠BEN=30°,
∵∠NEB+∠BEF=90°,
∴∠BEF=60°,
∴∠DEF=∠BED-∠BEF=90°-60°=30°,
∴∠DEF=∠CEM.
故答案为:90°;


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】七年级开展演讲比赛,学校决定购买一些笔记本和钢笔作为奖品.现有甲、乙两家商店出售两种同样的笔记本和钢笔.他们的定价相同:笔记本定价为每本25元,钢笔每支定价6元,但是他们的优惠方案不同,甲店每买一本笔记本赠一支钢笔;乙店全部按定价的9折优惠.已知七年级需笔记本20本,钢笔x支(大于20支).问:
(1)在甲店购买需付款 元,在乙店购买需付款 元;
(2)若x=30,通过计算说明此时到哪家商店购买较为合算?
(3)当x=40时,请设计一种方案,使购买最省钱?算出此时需要付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
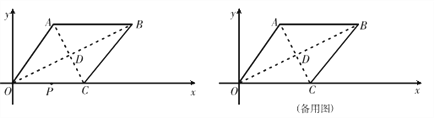
【题目】如图,在菱形 OA BC 中,已知点 B(8,4),C(5,0),
点 D 为 OB、AC 交点,点 P 从原点出发向 x 轴正方向运动;
(1) 在点 P 运动过程中,若∠OBP=900,求出点 P 坐标;
(2) 在点 P 运动过程中,若∠PDC+∠BCP=900,求出点 P 坐标;
(3) 点 P 在(2)的位置时停止运动,点 M 从点 P 出发沿 x 轴正方向运动,连结 BM,若点 P 关于BM 的对称点 P’到 AB 所在直线的距离为 2,求此时点 M 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D为边BC上一点,E为边AB的中点,过点A作AF∥BC,交DE的延长线于点F,连结BF.
(1)求证:四边形ADBF是平行四边形;
(2)当D为边BC的中点,且BC=2AC时,求证:四边形ACDF为正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中, AD// BC, ∠B=90°, AD=2, BC=5,E是AB上一点,将△BCE沿着直线CE翻折,点B恰好与点D重合,则BE=__

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在∠O的一边OA上.按要求画图并填空:

(1)过点A画直线AB ⊥OA,与∠O的另一边相交于点B;
(2)过点A画OB的垂线段AC,垂足为点C;
(3)过点C画直线CD∥OA ,交直线AB于点D;
(4)∠CDB= °;
(5)如果OA=8,AB=6,OB=10,则点A到直线OB的距离为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购进A,B两种树木共100棵进行校园绿化,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A,B两种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com