
【题目】已知:△ABC和△ADE均为等边三角形,连接BE,CD,点F,G,H分别为DE,BE,CD中点.
(1)当△ADE绕点A旋转时,如图1,则△FGH的形状为 ,说明理由;
(2)在△ADE旋转的过程中,当B,D,E三点共线时,如图2,若AB=3,AD=2,求线段FH的长;
(3)在△ADE旋转的过程中,若AB=a,AD=b(a>b>0),则△FGH的周长是否存在最大值和最小值,若存在,直接写出最大值和最小值;若不存在,说明理由.

【答案】(1)△FGH是等边三角形;(2)![]() ;(3)△FGH的周长最大值为
;(3)△FGH的周长最大值为![]() (a+b),最小值为
(a+b),最小值为![]() (a﹣b).
(a﹣b).
【解析】试题分析:(1)结论:△FGH是等边三角形.理由如下:根据三角形中位线定理证明FG=FH,再想办法证明∠GFH=60°即可解决问题;、
(2)如图2中,连接AF、EC.在Rt△AFE和Rt△AFB中,解直角三角形即可;
(3)首先证明△GFH的周长=3GF=![]() BD,求出BD的最大值和最小值即可解决问题;
BD,求出BD的最大值和最小值即可解决问题;
试题解析:解:(1)结论:△FGH是等边三角形.理由如下:
如图1中,连接BD、CE,延长BD交CE于M,设BM交FH于点O.
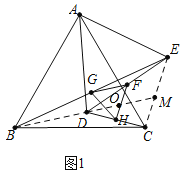
∵△ABC和△ADE均为等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE,∴∠BAD=∠CAE,∴△BAD≌△CAE,∴BD=CE,∠ADB=∠AEC,∵EG=GB,EF=FD,∴FG=![]() BD,GF∥BD,∵DF=EF,DH=HC,∴FH=
BD,GF∥BD,∵DF=EF,DH=HC,∴FH=![]() EC,FH∥EC,∴FG=FH,∵∠ADB+∠ADM=180°,∴∠AEC+∠ADM=180°,∴∠DMC+∠DAE=180°,∴∠DME=120°,∴∠BMC=60°
EC,FH∥EC,∴FG=FH,∵∠ADB+∠ADM=180°,∴∠AEC+∠ADM=180°,∴∠DMC+∠DAE=180°,∴∠DME=120°,∴∠BMC=60°
∴∠GFH=∠BOH=∠BMC=60°,∴△GHF是等边三角形,故答案为:等边三角形.
(2)如图2中,连接AF、EC.

易知AF⊥DE,在Rt△AEF中,AE=2,EF=DF=1,∴AF=![]() =
=![]() ,在Rt△ABF中,BF=
,在Rt△ABF中,BF=![]() =
=![]() ,∴BD=CE=BF﹣DF=
,∴BD=CE=BF﹣DF=![]() ,∴FH=
,∴FH=![]() EC=
EC=![]() .
.
(3)存在.理由如下.
由(1)可知,△GFH是等边三角形,GF=![]() BD,∴△GFH的周长=3GF=
BD,∴△GFH的周长=3GF=![]() BD,在△ABD中,AB=a,AD=b,∴BD的最小值为a﹣b,最大值为a+b,∴△FGH的周长最大值为
BD,在△ABD中,AB=a,AD=b,∴BD的最小值为a﹣b,最大值为a+b,∴△FGH的周长最大值为![]() (a+b),最小值为
(a+b),最小值为![]() (a﹣b).
(a﹣b).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=∠ACB=72°,CD平分∠ACB,则∠ADC=______.图中有______个等腰三角形,它们是:_________________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数x,y定义新运算:x*y=ax+by -5,其中a,b为常数.已知1*2=9,(-3)*3=-2,则a-b=
A.-1B.1C.-2D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
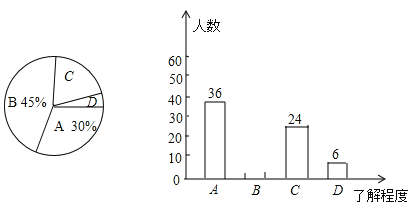
【题目】今年市委市政府积极推进创建“全国文明城市”工作,市创城办公室为了调查初中学生对“社会主义核心价值观”内容的了解程度(程度分为:“A﹣十分熟悉”,“B﹣了解较多”,“C﹣了解较少”,“D﹣不知道”),对我市一所中学的学生进行了随机抽样调查,根据调查结果绘制了两幅不完整的统计图如图,根据信息解答下列问题:
(1)本次抽样调查了多少名学生;
(2)补全条形统计图和扇形统计图;
(3)求扇形统计图中“D﹣不知道”所在的扇形圆心角的度数;
(4)若该中学共有2400名学生,请你估计这所中学的所有学生中,对“社会主义核心价值观”内容的了解程度为“十分熟悉”和“了解较多”的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点A、B的坐标分别是(a,0),(b,0)且![]() +|b-2|=0.
+|b-2|=0.
(1)求a、b的值;
(2)在y轴上是否存在点C,使三角形ABC的面积是12?若存在,求出点C的坐标;若不存在,请说明理由.
(3)已知点P是y轴正半轴上一点,且到x轴的距离为3,若点P沿平行于x轴的负半轴方向以每秒1个单位长度平移至点Q,当运动时间t为多少秒时,四边形ABPQ的面积S为15个平方单位?写出此时点Q的坐标. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超速行驶是一种十分危险的违法驾驶行为,在一条笔直的高速公路MN上,小型车限速为每小时120千米,设置在公路旁的超速监测点C,现测得一辆小型车在监测点C的南偏西30°方向的A处,7秒后,测得其在监测点C的南偏东45°方向的B处,已知BC=200米,B在A的北偏东75°方向,请问:这辆车超速了吗?通过计算说明理由.(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.

(1)出发2秒后,求△ABP的周长.
(2)问t满足什么条件时,△BCP为直角三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com