
| 3x |
| x-2 |
| x |
| x+2 |
| x2-4 |
| x |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2012-2013学年浙江建德市李家镇初级中学七年级5月单元检测数学卷(带解析) 题型:解答题
解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“长方形的长和宽的长分别是3和4,求长方形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若长方形的周长为14,且一边长为3,求另一边的长”;也可以是“若长方形的周长为14,求长方形面积的最大值”,等等.
(1)设 ,
,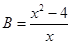 ,求A与B的积;
,求A与B的积;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏淮安涟水县南集中学七年级下学期期末考试数学卷(带解析) 题型:解答题
解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“长方形的长和宽的长分别是3和4,求长方形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若长方形的周长为14,且一边长为3,求另一边的长”;也可以是“若长方形的周长为14,求长方形面积的最大值”,等等.
(1)设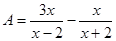 ,
, ,求A与B的积;
,求A与B的积;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
查看答案和解析>>
科目:初中数学 来源:2015届江苏淮安涟水县南集中学七年级下学期期末考试数学卷(解析版) 题型:解答题
解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“长方形的长和宽的长分别是3和4,求长方形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若长方形的周长为14,且一边长为3,求另一边的长”;也可以是“若长方形的周长为14,求长方形面积的最大值”,等等.
(1)设 ,
, ,求A与B的积;
,求A与B的积;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
查看答案和解析>>
科目:初中数学 来源:2015届浙江建德市七年级5月单元检测数学卷(解析版) 题型:解答题
解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“长方形的长和宽的长分别是3和4,求长方形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若长方形的周长为14,且一边长为3,求另一边的长”;也可以是“若长方形的周长为14,求长方形面积的最大值”,等等.
(1)设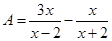 ,
, ,求A与B的积;
,求A与B的积;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com