
【题目】计算:
(1)![]() = ; (2)
= ; (2)![]() = ; (3)
= ; (3)![]() ;
;
(4)![]() ; (5)
; (5)![]() ; (6)a3·a3= ;
; (6)a3·a3= ;
(7) (x3)5= ; (8)(-2x2y3)3= ; (9) (x-y)6÷(x-y)3= ;
(10)a2b(ab-4b2) (11)(2a-3b)(2a+5b)
【答案】
(1)1.1;(2)![]() ;(3)-0.2;(4)5;(5)100 ;(6)a6;(7)x15;(8)-8x6y9;(9)(x-y)3;(10)a3b2-4a2b3;(11)4a2+4ab-15b2.
;(3)-0.2;(4)5;(5)100 ;(6)a6;(7)x15;(8)-8x6y9;(9)(x-y)3;(10)a3b2-4a2b3;(11)4a2+4ab-15b2.
【解析】
(1)根据算术平方根的定义计算即可;(2)根据平方根的定义计算即可;(3)根据立方根的定义计算即可;(4)根据二次根式的性质计算即可;(5)根据算术平方根的定义计算即可;(6)根据同底数幂的乘法法则计算即可;(7)根据幂的乘方的运算法则计算即可;(8)根据积的乘方的运算法则计算即可;(9)根据同底数幂的除法法则计算即可;(10)根据单项式乘以多项式的运算法则计算即可;(11)根据多项式乘以多项式的运算法则计算即可.
(1)![]() = 1.1;
= 1.1;
(2)![]() =
=![]() ;
;
(3)![]() -0.2;
-0.2;
(4)![]() 5;
5;
(5)![]() 100 ;
100 ;
(6)a3·a3=a6;
(7)(x3)5=x15;
(8)(-2x2y3)3=-8x6y9 ;
(9)(x-y)6÷(x-y)3=(x-y)3
(10)原式=a3b2-4a2b3;
(11)(2a-3b)(2a+5b)=4a2+10ab-6ab-15b2=4a2+4ab-15b2.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有几个?
(1)AE平分∠DAB;(2)△EBA≌△DCE; (3)AB+CD=AD;(4)AE⊥DE;(5)AB//CD;
大家一起热烈地讨论交流,小红第一个得出正确答案,是( ).

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于抛物线y=ax2﹣4ax+3a下列说法:①对称轴为x=2;②抛物线与x轴两交点的坐标分别为(1,0),(3,0);③顶点坐标为(2,﹣a);④若a<0,当x>2时,函数y随x的增大而增大,其中正确的结论有( )个.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,将正方形的边AD绕点A顺时针旋转到AE,连接BE、DE,过点A作AF⊥BE于F,交直线DE于P.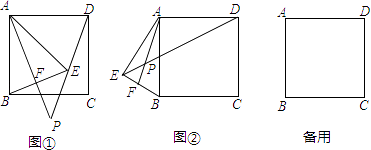
(1)如图①,若∠DAE=40°,求∠P的度数;
(2)如图②,若90°<∠DAE<180°,其它条件不变,试探究线段AP、DP、EP之间的数量关系,并说明理由;
(3)继续旋转线段AD,若旋转角180°<∠DAE<270°,则线段AP、DP、EP之间的数量关系为(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b图象经过点(1,3)和(4,6)
①试求![]() 与
与![]() ;
;

②画出这个一次函数图象;
③这个一次函数与y轴交点坐标是( )
④当x 时,y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题: 
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农庄计划在30亩空地上全部种植蔬菜和水果,菜农小张和果农小李分别承包了种植蔬菜和水果的任务,小张种植每亩蔬菜的工资y(元)与种植面积m(亩)之间的函数关系如图①所示,小李种植水果所得报酬z(元)与种植面积n(亩)之间的函数关系如图②所示
(1)如果种植蔬菜20亩,则小张种植每亩蔬菜的工资是元,小张应得的工资总额是元,此时,小李种植水果亩,小李应得的报酬是元;
(2)设农庄支付给小张和小李的总费用为W(元),当10<m<30时,求W与m之间的函数关系式,并求出总费用最大为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
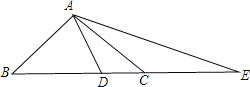
【题目】(1)如图,在在△ABC中,已知∠BAC=900,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,CE=CA,求∠DAE的度数;
(2)如果把(1)中的“AB=AC”条件去掉,其余条件不变,那么∠DAE的度数改变吗?为什么?
(3)如果把(1)中的“∠BAC=900”改成“∠BAC>900”其余条件不变,试探究∠DAE与∠BAC的数量关系式,试证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
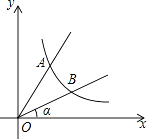
【题目】如图,直线y=2x与反比例函数y= ![]() (k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=
(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα= ![]() .
.
(1)求k的值.
(2)求点B的坐标.
(3)设点P(m,0),使△PAB的面积为2,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com