
分析 (1)求出判别式的值即可判定.△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.
(2)①利用配方法即可解决问题.
②当n=m2时,写出解析式,分三种情况减小讨论即可.
解答 解:(1)∵m=2,n=-3,
∴抛物线解析式为y=x2+2x-3,
∵△=22-4×1×(-3)=16>0,
∴抛物线y=x2+mx+n与x轴有两个交点.
(2)①n=m2时,抛物线解析式为y=x2+mx+m2=(x+$\frac{m}{2}$)2+$\frac{3}{4}$m2.
∴顶点P的坐标为($\frac{m}{2}$,$\frac{3}{4}$m2),
顶点P所在函数图象的解析式为,y=3x2.
②当n=m2时,二次函数解析式为y═x2+mx+m2,
图象开口向上,对称轴为直线x=-$\frac{m}{2}$,
①当-$\frac{m}{2}$<m,即m>0时,
在自变量x的值满足m≤x≤m+3的情况下,y随x的增大而增大,
∴当x=m时,y=m2+m•m+m2=3m2为最小值,
∴3m2=21,解得,m1=-$\sqrt{7}$(舍去),b2=$\sqrt{7}$;
②当m≤-$\frac{m}{2}$≤m+3时,即-2≤m≤0,
∴x=-$\frac{m}{2}$,y=$\frac{3}{4}$m2为最小值,
∴$\frac{3}{4}$m2=21,解得,m1=-2$\sqrt{7}$(舍去),b2=2$\sqrt{7}$(舍去);
③当-$\frac{m}{2}$>m+3,即m<-2,
在自变量x的值满足m≤x≤m+3的情况下,y随x的增大而减小,
故当x=m+3时,y=(m+3)2+m(m+3)+m2=3m2+9m+9为最小值,
∴3m2+9m+9=21.解得,m1=1(舍去),m2=-4;
∴m=$\sqrt{7}$时,解析式为:y=x2+$\sqrt{7}$x+7
b=-4时,解析式为:y=x2-4x+16.
综上可得,此时二次函数的解析式为y=x2+$\sqrt{7}$x+7或y=x2-4x+16.
点评 本题考查了二次函数的最值:当a>0时,抛物线在对称轴左侧,y随x的增大而减少;在对称轴右侧,y随x的增大而增大,因为图象有最低点,所以函数有最小值,当x=-$\frac{b}{2a}$时,y=$\frac{4ac-{b}^{2}}{4a}$;当a<0时,抛物线在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减少,因为图象有最高点,所以函数有最大值,当x=-$\frac{b}{2a}$时,y=$\frac{4ac-{b}^{2}}{4a}$;确定一个二次函数的最值,首先看自变量的取值范围,当自变量取全体实数时,其最值为抛物线顶点坐标的纵坐标;当自变量取某个范围时,要分别求出顶点和函数端点处的函数值,比较这些函数值,从而获得最值.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
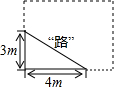 如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了4步路(假设2步为1米),却踩伤了花草.
如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了4步路(假设2步为1米),却踩伤了花草.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com