
【题目】某企业投资1000万元引进一条农产品生产线,若不计维修、保养费用,预计投产后每年可创330万元,该生产线投产后,从第一年到第x年的维修、保养费用累计为y(万元),且y=ax2+bx(a≠0),若第一年的维修、保养费为20万元,第二年的为40万元.
(1)求y与x之间的函数表达式;
(2)投产后,这个企业在第几年就能收回投资?
【答案】(1)y=10x2+10x(2)投产后该企业在第四年就能收回投资
【解析】
(1)根据条件解方程组易得解析式;
(2)收回投资即纯利润=投资(包括购设备、维修、保养).
(1)由题意,x=1时,y=20;
x=2时,y=20+40=60,分别代入y=ax2+bx
得![]()
解得:![]()
∴y=10x2+10x;
(2)设总利润为W元,则:W=330x﹣1000﹣10x2﹣10x,
则W=﹣10x2+320x﹣1000=﹣10(x﹣16)2+1560,
由于当1≤x≤16时,W 随的增大而增大,且当x=1、2、3时,W的值均小于0,
∴x=4时,W=﹣10×122+1560=120>0,
即投产后该企业在第四年就能收回投资.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为( )
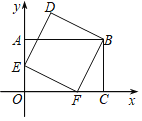
A. (1,2.5)B. (1,1+ ![]() )C. (1,3)D. (
)C. (1,3)D. (![]() ﹣1,1+
﹣1,1+ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(2m+4)x+(3﹣n).
(1)当m、n是什么数时,y随x的增大而增大;
(2)当m、n是什么数时,函数图象经过原点;
(3)若图象经过一、二、三象限,求m、n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y1=x2﹣4x+4的顶点为A,直线y2=kx﹣2k(k≠0),
(1)试说明直线是否经过抛物线顶点A;
(2)若直线y2交抛物线于点B,且△OAB面积为1时,求B点坐标;
(3)过x轴上的一点M(t,0)(0≤t≤2),作x轴的垂线,分别交y1,y2的图象于点P,Q,判断下列说法是否正确,并说明理由:
①当k>0时,存在实数t(0≤t≤2)使得PQ=3.
②当﹣2<k<﹣0.5时,不存在满足条件的t(0≤t≤2)使得PQ=3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在“我运动,我快乐”的技能比赛培训活动中,在相同条件下,对甲、乙两名同学的“单手运球”项目进行了5次测试,测试成绩(单位:分)如下:根据右图判断正确的是( )

A.甲成绩的平均分低于乙成绩的平均分;
B.甲成绩的中位数高于乙成绩的中位数;
C.甲成绩的众数高于乙成绩的众数;
D.甲成绩的方差低于乙成绩的方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:![]() 过点A(3,0),且与直线l2:
过点A(3,0),且与直线l2:![]() 交于点B(m,1).
交于点B(m,1).
(1)求直线l1:![]() 的函数表达式;
的函数表达式;
(2)过动点P(n,0)且垂于x轴的直线与l1、l2分别交于点C、D,当点C位于点D上方时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+3x+c经过A(﹣1,0),B(4,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)若点P在第一象限的抛物线上,且点P的横坐标为t,过点P向x轴作垂线交直线BC于点Q,设线段PQ的长为m,求m与t之间的函数关系式,并求出m的最大值;
(3)在x轴上是否存在点E,使以点B,C,E为顶点的三角形为等腰三角形?如果存在,直接写出E点坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张长20cm、宽12cm的矩形纸板,将纸板四个角各剪去一个边长为![]() cm的正方形,然后将四周突出部分折起,可制成一个无盖纸盒.
cm的正方形,然后将四周突出部分折起,可制成一个无盖纸盒.

(1)这个无盖纸盒的长为 cm,宽为 cm;(用含x的式子表示)
(2)若要制成一个底面积是180m2的无盖长方体纸盒,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com