
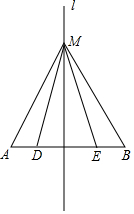
 如图所示,l是AB的中垂线,M是l上一点,D,E是AB上不同的两点,则AM=BM吗?MD=ME吗?
如图所示,l是AB的中垂线,M是l上一点,D,E是AB上不同的两点,则AM=BM吗?MD=ME吗? 分析 根据线段垂直平分线的定义得到∠AOM=∠BOM=90°,AO=BO,根据全等三角形的性质得到AM=BM,由于OD不一定等于OE,得不出DM=ME.
解答  解:AM=BM,DM不一定等于ME,
解:AM=BM,DM不一定等于ME,
理由:如图,∵l是AB的中垂线,
∴∠AOM=∠BOM=90°,
AO=BO,
在△AOM与△BOM中,$\left\{\begin{array}{l}{AO=BO}\\{∠AOM=∠BOM}\\{OM=OM}\end{array}\right.$,
∴AM=BM,
∵OD不一定等于OE,
∴△ODM与△OEM不一定全等,
∴DM不一定等于ME.
点评 本题考查了线段垂直平分线的性质,全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
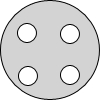 如图,在半径为R的圆形钢板上冲去半径r的四个小圆孔,若R=8.6cm,r=0.7cm,请你利用因式分解的方法计算出剩余钢板的面积.(π取3.14)
如图,在半径为R的圆形钢板上冲去半径r的四个小圆孔,若R=8.6cm,r=0.7cm,请你利用因式分解的方法计算出剩余钢板的面积.(π取3.14)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 商品名 | 单价(元) | 数量(个) | 金额(元) |
| 签字笔 | 3 | 2 | 6 |
| 自动铅笔 | 1.5 | ● | ● |
| 记号笔 | 4 | ● | ● |
| 软皮笔记本 | ● | 2 | 9 |
| 圆规 | 3.5 | 1 | ● |
| 合计 | 8 | 28 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com